Suorakulmaisten pulssien sähköiset ja ajalliset parametrit

Niitä kutsutaan yleensä jaksollisiksi ja ei-jaksollisiksi signaaleiksi, joiden muoto eroaa sinimuotoisista pulssisignaaleista... Pulssisignaalien generointi-, muunnos- ja kysymykset käytännön soveltamisesta liittyvät nykyään moniin elektroniikan alueisiin.

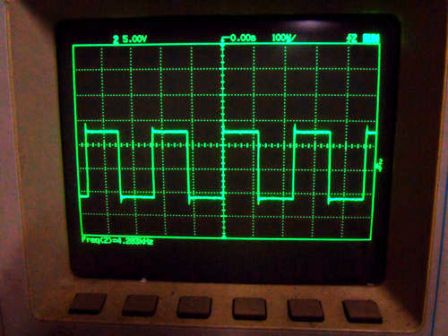
Joten esimerkiksi mikään nykyaikainen teholähde ei ole täydellinen ilman sen piirilevyllä olevaa neliöaaltogeneraattoria, kuten esimerkiksi TL494-mikropiirissä, joka tuottaa pulssijonoja, joiden parametrit sopivat virran kuormitukseen.

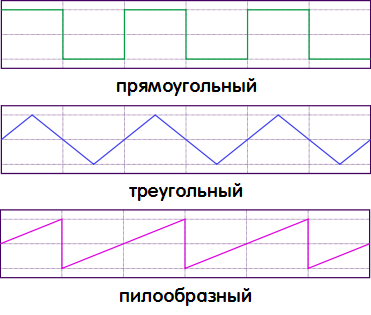
Koska pulssisignaaleilla voi olla erilainen muoto, ne kutsuvat erilaisia ​​pulsseja samanlaisen geometrisen muodon mukaan: suorakaiteen muotoisia pulsseja, puolisuunnikkaan muotoisia pulsseja, kolmiopulsseja, sahapulsseja, askelpulsseja ja monenlaisia ​​muita pulsseja. Samaan aikaan se on täsmälleen suorakaiteen muotoisia pulsseja... Niiden parametreja tarkastellaan tässä artikkelissa.

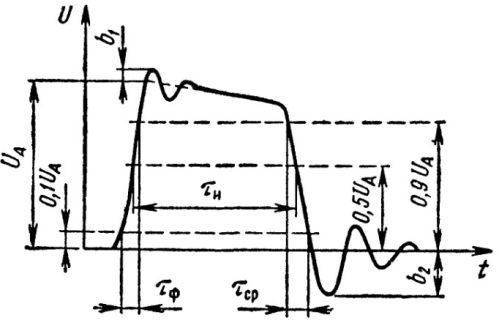
Tietenkin termi "suorakulmainen impulssi" on jonkin verran mielivaltainen. Johtuen siitä, että luonnossa ei ole mitään täydellistä, kuten ei ole täysin suorakaiteen muotoisia pulsseja.Itse asiassa todellisessa pulssissa, jota yleensä kutsutaan suorakaiteen muotoiseksi, voi myös olla värähteleviä aaltoja (esitetty kuvassa b1 ja b2), johtuen hyvin todellisista kapasitiivisista ja induktiivisista tekijöistä.

Nämä päästöt voivat tietysti puuttua, mutta pulsseilla on sähköisiä ja ajallisia parametreja, jotka heijastavat muun muassa "niiden suorakulmaisuuden epätäydellisyyttä".

Suorakaiteen muotoisella pulssilla on tietty napaisuus ja toimintataso. Useimmiten pulssin napaisuus on positiivinen, koska suurin osa digitaalisista mikropiireistä saa virtaa positiivisesta jännitteestä suhteessa yhteiseen johtimeen, ja siksi pulssin jännitteen hetkellinen arvo on aina suurempi kuin nolla.

Mutta on olemassa esimerkiksi kaksinapaisella jännitteellä toimivia vertailulaitteita; tällaisissa järjestelmissä voit löytää kaksisuuntaisia ​​pulsseja. Yleensä negatiivisen napaisuuden integroituja piirejä ei käytetä yhtä laajalti kuin tavanomaisia ​​positiivisen virran integroituja piirejä.

Pulssisarjassa pulssin käyttöjännite voi olla matala tai korkea, jolloin yksi taso korvaa toisen ajan myötä. Matala jännitetaso on merkitty U0:lla, korkea taso U1. Kutsutaan pulssin jännitteen korkeinta hetkellistä arvoa Ua tai Um suhteessa pulssiamplitudin alkutasoon.

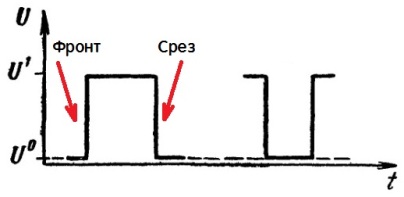
Pulssilaitteiden suunnittelijat työskentelevät usein korkean tason aktiivisten pulssien, kuten vasemmalla näkyvän, kanssa. Mutta joskus on käytännössä suositeltavaa käyttää aktiivisina matalan tason pulsseja, joiden alkutila on korkea jännitetaso. Matala pulssi näkyy oikealla olevassa kuvassa. Matalan tason impulssin kutsuminen "negatiiviseksi impulssiksi" on lukutaidottomia.

Suorakaiteen muotoisen pulssin jännitehäviötä kutsutaan frontiksi, joka edustaa nopeaa (aikasuhteessa piirissä tapahtuvan transienttiprosessin ajan kanssa) muutosta sähköisessä tilassa.

Matalasta korkeaan kaltevuutta eli positiivista kaltevuutta kutsutaan etureunaksi tai yksinkertaisesti pulssin reunaksi. Korkeasta matalaan tai negatiivista reunaa kutsutaan leikkaus-, kaltevuus- tai yksinkertaisesti pulssin takareunaksi. pulssi.

Etupää on merkitty tekstissä 0.1 tai kaavamaisesti _ | ja viimeinen 1.0 tai kaavamaisesti | _.

Aktiivisten elementtien inertiaominaisuuksista riippuen transienttiprosessi (dropout) todellisessa laitteessa vie aina jonkin verran aikaa. Siksi pulssin kokonaiskesto ei sisällä vain korkeiden ja alempien tasojen olemassaoloaikoja, vaan myös reunojen (alku- ja takareunojen) kestoajat, joita merkitään Tf:llä ja Tav:lla. Melkein missä tahansa kaaviossa nousu- ja laskuaika voidaan nähdä oskilloskooppi.

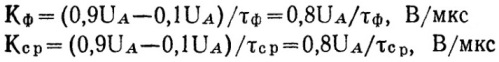
Koska todellisuudessa pisaroiden transienttien alkamis- ja loppuhetkeä ei ole helppo erottaa kovin tarkasti, on tapana pitää pudotuksen kestoa ajanjaksona, jonka aikana jännite muuttuu 0,1 Ua:sta 0,9 Ua:iin ( edessä) tai 0,9 Ua - 0,1 Ua (leikattu). Samoin etujyrkkyys Kf ja leikkausjyrkkyys Ks. on asetettu näiden rajatilojen mukaan ja mitataan voltteina mikrosekunnissa (V / μs). Pulssin kestoa kutsutaan aikaväliksi, joka lasketaan tasolta 0,5Ua.

Kun pulssien muodostumis- ja generointiprosesseja tarkastellaan kokonaisuutena, etuosan ja leikkaamisen oletetaan kestoltaan nollaksi, koska nämä pienet aikavälit eivät ole kriittisiä karkeiden laskelmien kannalta.

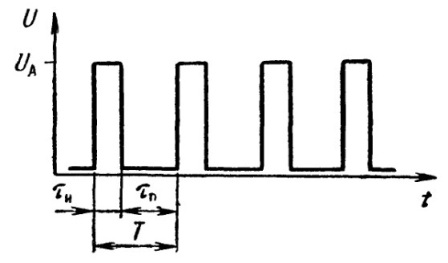
Pulssisekvenssi — nämä ovat pulsseja, jotka seuraavat toisiaan tietyssä järjestyksessä. Jos pulssien väliset tauot ja pulssien kesto sekvenssissä ovat yhtä suuret, kyseessä on jaksollinen sarja. Pulssin toistojakso T on pulssin keston ja pulssien välisen tauon summa sarjassa. Pulssin toistotaajuus f on jakson käänteisluku.

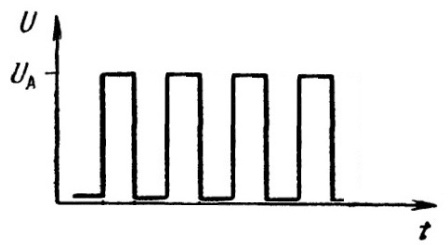
Suorakulmaisten pulssien jaksollisille sarjoille jakson T ja taajuuden f lisäksi on tunnusomaista useat lisäparametrit: toimintajakso DC ja toimintajakso Q. Toimintajakso on pulssin keston suhde sen jaksoon.

Hyvinvointi Pulssin jakson suhde sen kestoon. Jaksottaista toimintajaksoa Q = 2, eli sellaista, jossa pulssin leveys on yhtä suuri kuin pulssien välinen taukoaika tai jossa toimintajakso on DC = 0,5, kutsutaan neliöaaltoksi.