Jännitteiden, vastusten ja tehojen kolmiot

Jokainen, jolla on käsitys vektorikaavioista, huomaa helposti, että niistä voidaan erottaa hyvin selkeästi suorakulmainen jännitekolmio, jonka jokainen puoli heijastaa: piirin kokonaisjännitettä, aktiivivastuksen jännitettä ja jännitettä. reaktanssilla.

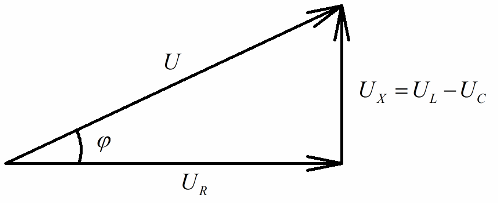
Pythagoraan lauseen mukaisesti näiden jännitteiden välinen suhde (piirin kokonaisjännitteen ja sen osien jännitteen välillä) näyttää tältä:

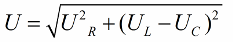
Jos seuraava vaihe on jakaa näiden jännitteiden arvot virralla (virta kulkee sarjapiirin kaikkien osien läpi tasaisesti), niin Ohmin laki saamme vastusarvot, eli nyt voimme puhua suorakulmaisesta vastusten kolmiosta:

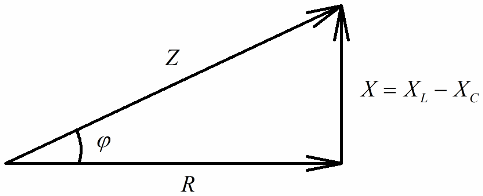
Samalla tavalla (kuten jännitteiden tapauksessa) Pythagoraan lausetta käyttämällä on mahdollista muodostaa suhde piirin impedanssin ja reaktanssien välille. Suhde ilmaistaan ​​seuraavalla kaavalla:

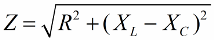
Sitten kerromme vastusarvot virralla, itse asiassa lisäämme oikean kolmion kutakin sivua tietyn määrän kertoja. Tuloksena saadaan suorakulmainen kolmio, jonka kapasiteetit:

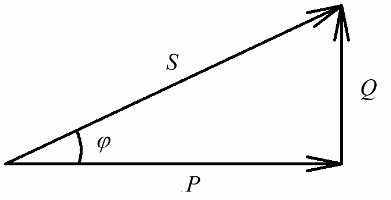
Sähköenergian palautumattomaan muuntamiseen (lämmöksi, laitoksessa suoritettaessa) liittyvän piirin aktiivivastuksen yhteydessä vapautuva pätöteho on selvästi yhteydessä energian palautuvaan muuntamiseen (luomiseen) liittyvään loistehoon. magneetti- ja sähkökentät keloissa ja kondensaattoreissa) ja täydellä teholla sähköasennukseen.

Aktiivinen teho mitataan watteina (W), loisteho — varissa (VAR — volttiampeeri loisteho), kokonaismäärä — VA:na (volt-ampeere).

Pythagoraan lauseen mukaan meillä on oikeus kirjoittaa:

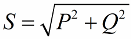
Kiinnitetään nyt huomiota siihen, että tehokolmiossa on kulma phi, jonka kosini on helppo määrittää ensisijaisesti pätöteholla ja näennäisteholla. Tämän kulman kosini (cos phi) kutsutaan tehokertoimeksi. Se näyttää kuinka suuri osa kokonaistehosta kuluu sähköasennuksessa tehtäessä hyödyllistä työtä, eikä sitä palauteta verkkoon.

Ilmeisesti suurempi tehokerroin (enintään yksi) osoittaa laitokselle toimitetun energian suurempaa muunnostehokkuutta. Jos tehokerroin on 1, kaikki syötetty energia käytetään työhön.

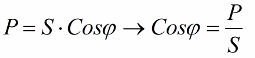
Saatujen suhteiden avulla voidaan ilmaista laitteiston virrankulutus tehokertoimella, pätöteholla ja verkkojännitteellä:

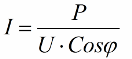
Joten mitä pienempi kosini phi on, sitä enemmän verkko tarvitsee virtaa tietyn työn suorittamiseen. Käytännössä tämä tekijä (verkon maksimivirta) rajoittaa siirtojohdon siirtokapasiteettia ja siksi mitä pienempi tehokerroin, sitä suurempi on linjan kuormitus ja pienempi hyödyllinen kaistanleveys (pieni kosini phi johtaa rajoitukseen). Joulehäviöt voimalinjoissa, joiden kosini phi pienenee, voidaan nähdä seuraavasta kaavasta:

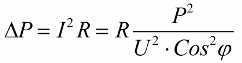
Voimajohdon aktiivisella resistanssilla R häviöt kasvavat mitä suurempi virta I on, vaikka se reagoi kuormaan. Siksi voimme sanoa, että alhaisella tehokertoimella sähkönsiirron kustannukset yksinkertaisesti kasvavat. Tämä tarkoittaa, että kosini phi:n kasvattaminen on tärkeä kansantaloudellinen tehtävä.

On toivottavaa, että kokonaistehon loiskomponentti lähestyy nollaa, joten sähkömoottoreita ja muuntajia olisi hyvä käyttää aina täydellä kuormituksella ja sammuttaa ne käytön lopussa, jotta ne eivät käy tyhjäkäynnillä. Kuormittamattomana moottoreilla ja muuntajilla on erittäin pieni tehokerroin. Yksi tapa lisätä kosini-phi-arvoa käyttäjissä on käyttää kondensaattoripankit ja synkroniset kompensaattorit.