Sähkökenttä, sähköstaattinen induktio, kapasitanssi ja kondensaattorit

Sähkökentän käsite

Sähkökenttävoimien tiedetään vaikuttavan sähkövarauksia ympäröivässä tilassa. Lukuisat kokeet varautuneilla kappaleilla vahvistavat tämän täysin. Varautuneen kappaleen ympärillä oleva tila on sähkökenttä, jossa sähkövoimat vaikuttavat.

Kenttävoimien suuntaa kutsutaan sähkökenttäviivoiksi. Siksi on yleisesti hyväksyttyä, että sähkökenttä on joukko voimalinjoja.

Kenttärivillä on tiettyjä ominaisuuksia:

• voimalinjat lähtevät aina positiivisesti varautuneesta kappaleesta ja menevät negatiivisesti varautuneeseen kappaleeseen;

• ne poistuvat kaikkiin suuntiin kohtisuoraan varautuneen kappaleen pintaan nähden ja tulevat siihen kohtisuorasti;

• kahden yhtä varautuneen kappaleen voimalinjat näyttävät hylkivän toisiaan ja vastakkaisesti varautuneet kappaleet vetävät puoleensa.

Sähkökenttävoimalinjat ovat aina auki, kun ne katkeavat varautuneiden kappaleiden pinnalla.Sähköisesti varautuneet kappaleet ovat vuorovaikutuksessa: vastakkaisesti varautuneet vetävät puoleensa ja samalla tavalla hylkivät.

Sähköisesti varatut kappaleet (hiukkaset), joiden varaukset ovat q1 ja q2, ovat vuorovaikutuksessa toistensa kanssa voimalla F, joka on vektorisuure ja mitataan newtoneina (N). Vastakkaiset varaukset vetävät toisiaan puoleensa ja samalla varauksella hylkivät toisiaan.

Vetovoima tai hylkiminen riippuu kappaleiden varausten suuruudesta ja niiden välisestä etäisyydestä.

Varautuneita kappaleita kutsutaan pisteiksi, jos niiden lineaariset mitat ovat pienet verrattuna kappaleiden väliseen etäisyyteen r. Niiden vuorovaikutusvoiman F suuruus riippuu varausten q1 ja q2 suuruudesta, niiden välisestä etäisyydestä r ja ympäristöstä, jossa sähkövaraukset sijaitsevat.

Jos kappaleiden välisessä tilassa ei ole ilmaa, vaan jotain muuta eristettä eli sähköä ei-johtavaa, kappaleiden välinen vuorovaikutusvoima pienenee.

Eristeen ominaisuuksia kuvaavaa arvoa, joka osoittaa, kuinka monta kertaa varausten välinen vuorovaikutusvoima kasvaa, jos tietty eriste korvataan ilmalla, kutsutaan tietyn dielektrin suhteelliseksi permittiivisyydeksi.

Dielektrisyysvakio on yhtä suuri kuin: ilma ja kaasut — 1; eboniitille - 2 - 4; kiillelle 5 - 8; öljylle 2-5; paperille 2 — 2,5; parafiinille — 2 — 2,6.

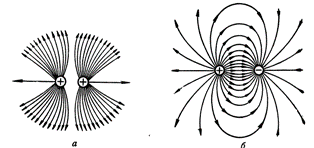
Kahden varautuneen kappaleen sähköstaattinen kenttä: a — talat ovat varautuneet samalla nimellä, b — kappaleet varautuvat eri tavalla

Sähköstaattinen induktio

Jos johtavalle kappaleelle A, jolla on pallomainen muoto, joka on eristetty ympäröivistä esineistä, annetaan negatiivinen sähkövaraus eli ylimäärä elektroneja luodaan siihen, tämä varaus jakautuu tasaisesti kehon pinnalle.Tämä johtuu siitä, että elektronit, jotka hylkivät toisiaan, pyrkivät tulemaan kehon pinnalle.

Sijoitamme varaamattoman kappaleen B, joka on myös eristetty ympäröivistä esineistä, kappaleen A kenttään. Tällöin kappaleen B pinnalle ilmaantuu sähkövarauksia ja kappaleen A puoleiselle puolelle varaus, joka on vastakkainen kappaleen A varauksen kanssa ( positiivinen ), ja toisella puolella - varaus, jolla on sama nimi kuin kehon A varaus (negatiivinen). Näin jakautuneet sähkövaraukset jäävät kappaleen B pinnalle sen ollessa kappaleen A kentässä. Jos kappale B poistetaan kentästä tai kappale A poistetaan, niin kappaleen B pinnalla oleva sähkövaraus neutraloituu. Tätä kaukaa tapahtuvaa sähköistämismenetelmää kutsutaan sähköstaattiseksi induktioksi tai sähköistymiseksi vaikutuksen avulla.

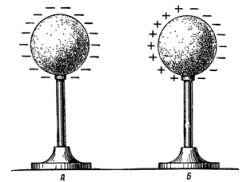
Sähköstaattisen induktion ilmiö

On selvää, että tällainen kehon sähköistetty tila pakotetaan ja ylläpidetään yksinomaan kappaleen A luoman sähkökentän voimien vaikutuksesta.

Jos teemme samoin, kun kappale A on positiivisesti varautunut, niin ihmisen käden vapaat elektronit ryntäävät kappaleeseen B, neutraloivat sen positiivisen varauksen ja kappale B varautuu negatiivisesti.

Mitä korkeampi on kappaleen A sähköistysaste, eli mitä suurempi sen potentiaali on, sitä suurempi potentiaali voidaan sähköistää sähköstaattisen induktiokappaleen B avulla.

Siten tulimme siihen tulokseen, että sähköstaattisen induktion ilmiö mahdollistaa tietyissä olosuhteissa akkumuloinnin sähköä johtavien kappaleiden pinnalla.

Mikä tahansa keho voidaan ladata tiettyyn rajaan, toisin sanoen tiettyyn potentiaaliin; potentiaalin lisääntyminen rajan yli aiheuttaa kehon sinkoutumisen ympäröivään ilmakehään. Eri kehot tarvitsevat eri määriä sähköä saattaakseen ne samaan potentiaaliin. Toisin sanoen eri kappaleet sisältävät eri määriä sähköä, eli niillä on erilaiset sähköiset kapasiteetit (tai yksinkertaisesti kapasiteetit).

Sähköinen kapasiteetti on kehon kyky sisältää tietyn määrän sähköä ja samalla nostaa sen potentiaalia tiettyyn arvoon. Mitä suurempi kehon pinta-ala, sitä enemmän sähkövarausta se voi pitää.

Jos runko on pallon muotoinen, sen kapasiteetti on suoraan verrannollinen pallon säteeseen. Kapasitanssi mitataan faradeina.

Farada on sellaisen kappaleen kapasiteetti, joka vastaanotettuaan sähkövarauksen riipuksessa lisää potentiaaliaan yhdellä voltilla... 1 farad = 1 000 000 mikrofaradia.

Sähkökapasiteettia, eli johtavien kappaleiden kykyä kerätä sähkövarausta itsessään, käytetään laajalti sähkötekniikassa. Laite perustuu tähän ominaisuuteen sähköiset kondensaattorit.

Kondensaattorin kapasitanssi

Kondensaattori koostuu kahdesta metallilevystä (levystä), jotka on eristetty toisistaan ​​ilmakerroksella tai muulla eristeellä (kiille, paperi jne.).

Jos yhdelle levyistä annetaan positiivinen varaus ja toinen on negatiivinen, eli varaa ne vastakkaisesti, levyjen toisiaan puoleensa vetävät varaukset pysyvät levyillä. Tämä mahdollistaa paljon enemmän sähkön keskittymisen levyihin kuin jos ne ladattaisiin etäällä toisistaan.

Siksi kondensaattori voi toimia laitteena, joka varastoi levyihinsä merkittävän määrän sähköä. Toisin sanoen kondensaattori on sähköenergian varastointi.

Kondensaattorin kapasitanssi on yhtä suuri kuin:

C = eS / 4pl

jossa C on kapasitanssi; e on eristeen dielektrisyysvakio; S - yhden levyn pinta-ala cm2, NS - vakioluku (pi) on 3,14; l - levyjen välinen etäisyys cm.

Tästä kaavasta voidaan nähdä, että kun levyjen pinta-ala kasvaa, kondensaattorin kapasiteetti kasvaa, ja kun niiden välinen etäisyys kasvaa, se pienenee.

Selitetään tämä riippuvuus. Mitä suurempi levyjen pinta-ala, sitä enemmän ne voivat imeä sähköä ja siksi kondensaattorin kapasiteetti on suurempi.

Levyjen välisen etäisyyden pienentyessä niiden varausten välinen keskinäinen vaikutus (induktio) kasvaa, mikä mahdollistaa enemmän sähkön keskittämisen levyihin ja siten kondensaattorin kapasiteetin lisäämisen.

Siten, jos haluamme saada suuren kondensaattorin, meidän on otettava levyt, joilla on suuri pinta-ala ja eristettävä ne ohuella dielektrisellä kerroksella.

Kaava osoittaa myös, että kun eristeen dielektrisyysvakio kasvaa, kondensaattorin kapasitanssi kasvaa.

Siksi kondensaattoreilla, joilla on samat geometriset mitat, mutta jotka sisältävät eri dielektrisiä aineita, on erilaiset kapasitanssit.

Jos esimerkiksi otamme kondensaattorin, jossa on ilmadielektrisyys, jonka dielektrisyysvakio on yhtä suuri kuin yksi, ja laitamme sen levyjen väliin kiillettä, jonka dielektrisyysvakio on 5, niin kondensaattorin kapasitanssi kasvaa 5-kertaiseksi.

Siksi materiaaleja, kuten kiille, parafiinilla kyllästetty paperi jne., joiden dielektrisyysvakio on paljon korkeampi kuin ilman, käytetään eristeenä suuren kapasiteetin saavuttamiseksi.

Tämän mukaisesti erotetaan seuraavat kondensaattorityypit: ilma, kiinteä dielektrinen ja nestemäinen dielektrinen.

Kondensaattorin lataus ja purkaminen. Bias-virta

Sisällytetään piiriin vakiokapasitanssin kondensaattori. Kun kytkin asetetaan koskettimeen a, kondensaattori liitetään akkupiiriin. Miliammetrin neula sillä hetkellä, kun kondensaattori on kytketty piiriin, poikkeaa ja muuttuu sitten nollaksi.

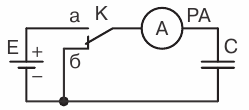
DC-kondensaattori

Siksi sähkövirta kulki piirin läpi tiettyyn suuntaan. Jos kytkin asetetaan nyt koskettimeen b (eli sulje levyt), milliammetrin neula poikkeaa toiseen suuntaan ja palaa nollaan. Siksi virta kulki myös piirin läpi, mutta eri suuntaan. Analysoidaan tämä ilmiö.

Kun kondensaattori kytkettiin akkuun, se latautui, eli sen levyt saivat yhden positiivisen ja toisen negatiivisen varauksen. Laskutus jatkuu asti mahdollinen eroavaisuus kondensaattorilevyjen välillä ei ole yhtä suuri kuin akun jännite. Piirissä sarjaan kytketty milliampeerimittari ilmaisee kondensaattorin latausvirran, joka pysähtyy välittömästi kondensaattorin latautumisen jälkeen.

Kun kondensaattori irrotettiin akusta, se pysyi ladattuna ja sen levyjen välinen potentiaaliero oli yhtä suuri kuin akun jännite.

Heti kun kondensaattori kuitenkin suljettiin, se alkoi purkautua ja purkausvirta kulki piirin läpi, mutta jo vastakkaiseen suuntaan kuin latausvirta. Tämä jatkuu, kunnes levyjen välinen potentiaaliero katoaa, eli kunnes kondensaattori purkautuu.

Siksi, jos kondensaattori sisältyy DC-piiriin, virta virtaa piirissä vain kondensaattorin latauksen aikana, ja jatkossa piirissä ei ole virtaa, koska dielektri rikkoo piirin. kondensaattorista.

Siksi he sanovat, että "kondensaattori ei läpäise tasavirtaa".

Kondensaattorin levyille keskittävissä oleva sähkön määrä (Q), sen kapasiteetti (C) ja kondensaattoriin syötettävän jännitteen arvo (U) liittyvät seuraavaan suhteeseen: Q = CU.

Tämä kaava osoittaa, että mitä suurempi kondensaattorin kapasiteetti, sitä enemmän siihen voidaan keskittää sähköä lisäämättä merkittävästi sen levyjen jännitettä.

DC-kapasitanssijännitteen lisääminen lisää myös kondensaattorin varastoiman sähkön määrää. Kuitenkin, jos kondensaattorin levyihin syötetään suuri jännite, kondensaattori voi "särkyä", eli tämän jännitteen vaikutuksesta eriste romahtaa jossain paikassa ja päästää virran kulkemaan sen läpi. Tässä tapauksessa kondensaattori lakkaa toimimasta. Kondensaattorien vaurioitumisen välttämiseksi ne osoittavat sallitun käyttöjännitteen arvon.

Dielektrisen polarisaation ilmiö

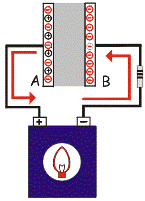Analysoidaan nyt, mitä tapahtuu dielektrissä, kun kondensaattoria ladataan ja puretaan, ja miksi kapasitanssin arvo riippuu dielektrisyysvakiosta?

Vastaus tähän kysymykseen antaa meille elektronisen teorian aineen rakenteesta.

Dielektrissä, kuten missä tahansa eristeessä, ei ole vapaita elektroneja. Eristeen atomeissa elektronit ovat tiukasti sidottu ytimeen, joten kondensaattorin levyihin kohdistuva jännite ei aiheuta elektronien suuntaista liikettä sen eristeessä, ts. sähkövirta, kuten johtojen tapauksessa.

Kuitenkin varautuneiden levyjen synnyttämien sähkökenttävoimien vaikutuksesta atomiytimen ympärillä pyörivät elektronit siirtyvät kohti positiivisesti varautunutta kondensaattorilevyä. Samalla atomi venyy kenttälinjojen suuntaan, tätä dielektristen atomien tilaa kutsutaan polarisoiduksi ja itse ilmiötä dielektriseksi polarisaatioksi.

Kondensaattorin purkauduttua eristeen polarisoitunut tila katkeaa, eli polarisaation aiheuttama elektronien siirtymä ytimeen nähden katoaa ja atomit palaavat tavanomaiseen polarisoimattomaan tilaan. Todettiin, että eriste heikentää kenttää kondensaattorin levyjen välillä.

Eri eristeet saman sähkökentän vaikutuksesta polarisoituvat eriasteisesti. Mitä helpommin eriste polarisoituu, sitä enemmän se heikentää kenttää. Esimerkiksi ilman polarisaatio johtaa vähemmän kentän heikkenemiseen kuin minkään muun eristeen polarisaatio.

Mutta kondensaattorin levyjen välisen kentän heikkeneminen antaa sinun keskittyä niihin suuremman määrän sähköä Q samalla jännitteellä U, mikä puolestaan ​​​​johtaa kondensaattorin kapasiteetin kasvuun, koska C = Q / U .

Joten päädyimme siihen johtopäätökseen - mitä suurempi eristeen dielektrisyysvakio on, sitä suurempi on sen kondensaattorin kapasiteetti, joka sisältää tämän dielektrisen koostumuksessaan.

Elektronien siirtymä eristeen atomeissa, joka tapahtuu, kuten olemme jo sanoneet, sähkökentän voimien vaikutuksesta, muodostuu eristeessä, kentän toiminnan ensimmäisellä hetkellä, sähköinen virta . Kutsutaan poikkeutusvirraksi... Se on saanut nimensä, koska toisin kuin metallilankojen johtavuusvirta, siirtymävirta syntyy vain niiden atomeissa liikkuvien elektronien siirtymisestä.

Tämän bias-virran läsnäolo saa vaihtovirtalähteeseen kytketystä kondensaattorista sen johtimen.

Katso myös tästä aiheesta: Sähkö- ja magneettikenttä: mitkä ovat erot?

Sähkökentän pääominaisuudet ja väliaineen tärkeimmät sähköiset ominaisuudet (perustermit ja määritelmät)

Sähkökentän voimakkuus

Vektorisuure, joka luonnehtii sähkökentän voimavaikutusta sähköisesti varautuneisiin kappaleisiin ja hiukkasiin ja joka on yhtä suuri kuin sen voiman suhteen raja, jolla sähkökenttä vaikuttaa paikallaan olevaan pistevarautuneeseen kappaleeseen, joka tuodaan tarkasteltavassa kentän kohdassa tämän kappaleen varaus, kun tämä varaus pyrkii nollaan ja jonka suunnan oletetaan olevan sama kuin positiivisesti varautuneeseen pistekappaleeseen vaikuttavan voiman suunta.

Sähkökenttäviiva

Suora missä tahansa pisteessä, jonka tangentti on sama kuin sähkökentän voimakkuusvektorin suunta.

Sähköinen polarisaatio

Aineen olotila, jolle on tunnusomaista se, että kyseisen aineen tietyn tilavuuden sähkömomentti on arvoltaan muu kuin nolla.

Sähkönjohtavuus

Aineen ominaisuus johtaa ajassa muuttumattoman sähkökentän vaikutuksesta sähkövirtaa, joka ei muutu ajassa.

Dielektrinen

Aine, jonka tärkein sähköinen ominaisuus on kyky polarisoitua sähkökentässä ja jossa sähköstaattisen kentän pitkäaikainen olemassaolo on mahdollista.

Johtava aine

Aine, jonka tärkein sähköinen ominaisuus on sähkönjohtavuus.

Johtaja

Johtava runko.

Puolijohdeaine (puolijohde)

Aine, jonka sähkönjohtavuus on johtavan aineen ja eristeen välissä ja jonka erottavia ominaisuuksia ovat: sähkönjohtavuuden voimakas riippuvuus lämpötilasta; sähkönjohtavuuden muutos sähkökentässä, valossa ja muissa ulkoisissa tekijöissä; sen sähkönjohtavuuden merkittävä riippuvuus lisättyjen epäpuhtauksien määrästä ja luonteesta, mikä mahdollistaa sähkövirran vahvistamisen ja korjaamisen sekä joidenkin energiatyyppien muuntamisen sähköksi.

Polarisaatio (polarisaation intensiteetti)

Vektorisuure, joka kuvaa dielektrisen sähköisen polarisaatioastetta, joka on yhtä suuri kuin eristeen tietyn tilavuuden sähkömomentin suhteen raja tähän tilavuuteen, kun jälkimmäinen pyrkii nollaan.

Sähkövakio

Onkalossa olevaa sähkökenttää kuvaava skalaarisuure, joka on yhtä suuri kuin tietyn suljetun pinnan sisältämän kokonaissähkövarauksen suhde sähkökentän voimakkuusvektorin virtaukseen tämän pinnan läpi tyhjässä.

Absoluuttinen dielektrinen herkkyys

Skalaarisuure, joka kuvaa eristeen ominaisuutta polarisoitua sähkömassassa ja joka on yhtä suuri kuin polarisaation suuruuden suhde sähkökentän voimakkuuden suuruuteen.

Dielektrinen herkkyys

Absoluuttisen dielektrisen susceptibilisuuden suhde dielektrisen tarkastelun pisteessä sähkövakioon.

Sähköinen siirtymä

Vektorisuure, joka on yhtä suuri kuin tarkastelupisteen sähkökentän voimakkuuden geometrinen summa kerrottuna sähkövakiolla ja polarisaatiolla samassa pisteessä.

Absoluuttinen dielektrisyysvakio

Dielektrin sähköisiä ominaisuuksia kuvaava skalaarisuure, joka on yhtä suuri kuin sähkösiirtymän suuruuden suhde sähkökentän jännitteen suuruuteen.

Dielektrisyysvakio

Dielektrisen tarkastelun pisteen absoluuttisen dielektrisyysvakion suhde sähkövakioon.

Siirtovoimalinja

Suora, jonka jokaisessa pisteessä sen tangentti on sama kuin sähköisen siirtymävektorin suunta.

Sähköstaattinen induktio

Ilmiö sähkövarausten induktiosta johtavassa kappaleessa ulkoisen sähköstaattisen kentän vaikutuksesta.

Kiinteä sähkökenttä

Sähkövirtojen sähkökenttä, joka ei muutu ajassa, edellyttäen, että virtaa kuljettavat johtimet ovat paikallaan.

Potentiaalinen sähkökenttä

Sähkökenttä, jossa sähkökentän voimakkuusvektorin roottori on kaikkialla nolla.

Pyörteinen sähkökenttä

Sähkökenttä, jossa intensiteettivektorin roottori ei aina ole nolla.

Sähköpotentiaalien ero kahdessa pisteessä

Potentiaalista sähkökenttää kuvaava skalaarisuure, joka on yhtä suuri kuin tämän kentän voimien työn suhteen raja, kun positiivisesti varautunut pistekappale siirretään kentän tietystä pisteestä toiseen, tämän kappaleen varaukseen , kun kehon varaus pyrkii nollaan (muuten: yhtä suuri kuin sähkökentän voimakkuuden viivaintegraali pisteestä toiseen).

Sähköinen potentiaali tietyssä pisteessä

Tietyn pisteen ja toisen määritellyn mutta mielivaltaisesti valitun pisteen sähköpotentiaalien välinen ero.

Yhden johtimen sähköinen kapasitanssi

Skalaarisuure, joka kuvaa johtimen kykyä kerätä sähkövarausta, yhtä suuri kuin johtimen varauksen suhde sen potentiaaliin, olettaen, että kaikki muut johtimet ovat äärettömän kaukana ja että äärettömän kaukaisen pisteen potentiaalin oletetaan olevan nolla.

Sähköinen kapasitanssi kahden yksittäisen johtimen välillä

Skalaariarvo, joka on yhtä suuri kuin yhden johtimen sähkövarauksen ja kahden johtimen sähköpotentiaalien välisen suhteen absoluuttinen arvo edellyttäen, että näiden johtimien suuruus on sama, mutta etumerkillisesti vastakkainen ja että kaikki muut johtimet ovat äärettömän kaukana.

Lauhdutin

Kahden johtimen (levyn) järjestelmä, jotka on erotettu eristeellä, joka on suunniteltu käyttämään kahden johtimen välistä kapasitanssia.

Kondensaattorin kapasitanssi

Yhden kondensaattorilevyn sähkövarauksen ja niiden välisen potentiaalieron suhteen absoluuttinen arvo edellyttäen, että levyillä on samansuuruiset ja vastakkaiset varaukset.

Kapasitanssi kahden johtimen välillä johdinjärjestelmässä (osittainen kapasitanssi)

Yhden johdinjärjestelmään kuuluvan johtimen sähkövarauksen suhteen absoluuttinen arvo sen ja toisen johtimen väliseen potentiaalieroon, jos kaikilla johtimilla, paitsi jälkimmäisellä, on sama potentiaali; jos maa sisältyy tarkasteltuun johtojärjestelmään, sen potentiaali on nolla.

Kolmannen osapuolen sähkökenttä

Termisten prosessien, kemiallisten reaktioiden, kosketusilmiöiden, mekaanisten voimien ja muiden ei-sähkömagneettisten (makroskooppisessa tutkimuksessa) prosessien aiheuttama kenttä; jolle on ominaista voimakas vaikutus varautuneisiin hiukkasiin ja kappaleisiin, jotka sijaitsevat alueella, jolla tämä kenttä on.

Indusoitu sähkökenttä

Ajassa muuttuvan magneettikentän indusoima sähkökenttä.

Sähkömoottorivoima E.d.S.

Skalaarisuure, joka kuvaa ulkoisen ja indusoidun sähkökentän kykyä indusoida sähkövirta, joka on yhtä suuri kuin ulkoisten ja indusoituneiden sähkökenttien voimakkuuden lineaarinen integraali kahden pisteen välillä tarkasteltavalla polulla tai pitkin tarkasteltua suljettua piiriä.

Jännite

Skalaarisuure, joka on yhtä suuri kuin tuloksena olevan sähkökentän voimakkuuden lineaarinen integraali (sähköstaattinen, kiinteä, ulkoinen, induktiivinen) kahden tarkasteltavalla polulla olevan pisteen välillä.