Johtojen sähkövastus
Sähkövastuksen ja johtavuuden käsite
Jokaisella kappaleella, jonka läpi sähkövirta kulkee, on tietty vastus sille. Johtavan materiaalin ominaisuutta estää sähkövirtaa kulkemasta sen läpi kutsutaan sähkövastukseksi.
Elektroniikkateoria selittää metallijohtimien sähkövastuksen luonteen tällä tavalla. Vapaat elektronit, liikkuessaan johtoa pitkin, kohtaavat matkallaan atomeja ja muita elektroneja lukemattomia kertoja ja vuorovaikutuksessa niiden kanssa väistämättä menettävät osan energiastaan. Elektronit kokevat vastustusta liikkeelleen joka tapauksessa. Eri metallijohtimilla, joilla on erilaiset atomirakenteet, on erilainen sähkövirran vastus.
Täsmälleen sama selittää nestejohtimien ja kaasujen vastuksen sähkövirran kulkua vastaan. Emme kuitenkaan saa unohtaa, että näissä aineissa elektronit eivät, vaan molekyylien varautuneet hiukkaset kohtaavat vastusta liikkuessaan.
Resistanssi on merkitty latinalaisilla kirjaimilla R tai r.
Ohmi otetaan sähkövastuksen yksikkönä.
Ohm on 106,3 cm korkean elohopeapylvään resistanssi, jonka poikkileikkaus on 1 mm2 0 °C:n lämpötilassa.
Jos esimerkiksi johdon sähkövastus on 4 ohmia, niin se kirjoitetaan näin: R = 4 ohmia tai r = 4 th.
Suurten vastusten mittaamiseen käytetään yksikköä, jota kutsutaan megaohmiksi.
Yksi megaohmi vastaa miljoonaa ohmia.
Mitä suurempi langan vastus on, sitä huonommin se johtaa sähkövirtaa, ja päinvastoin, mitä pienempi langan vastus, sitä helpompi sähkövirran kulkee tämän johdon läpi.
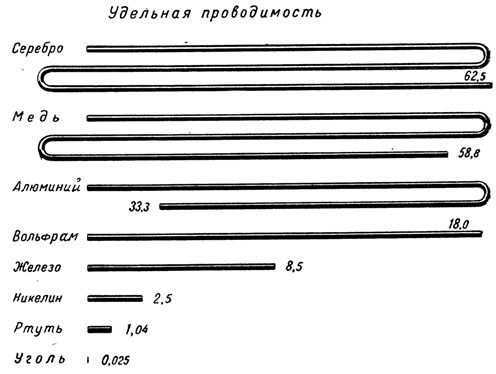
Siksi johtimen ominaisuuksien osalta (sähkövirran kulkemisen kannalta sen läpi) voidaan ottaa huomioon paitsi sen resistanssi, myös resistanssin käänteisarvo, jota kutsutaan johtavuudelle.

Sähkönjohtavuudella tarkoitetaan materiaalin kykyä siirtää sähkövirtaa itsensä läpi.
Koska konduktanssi on resistanssin käänteisluku, se ilmaistaan muodossa 1 /R, konduktanssi on merkitty latinalaisella kirjaimella g.
Johtimen materiaalin, sen mittojen ja ympäristön lämpötilan vaikutus sähkövastuksen arvoon
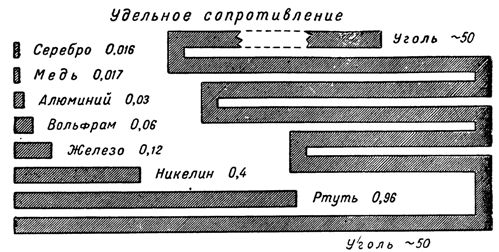
Eri johtojen resistanssi riippuu materiaalista, josta ne on valmistettu. Eri materiaalien sähkövastuksen karakterisoimiseksi käsite ns Resistanssi.
 Resistanssia kutsutaan langan resistanssiksi, jonka pituus on 1 m ja poikkipinta-ala 1 mm2. Resistanssi on merkitty kreikkalaisella kirjaimella r. Jokaisella materiaalilla, josta johdin on valmistettu, on oma ominaisvastus.
Resistanssia kutsutaan langan resistanssiksi, jonka pituus on 1 m ja poikkipinta-ala 1 mm2. Resistanssi on merkitty kreikkalaisella kirjaimella r. Jokaisella materiaalilla, josta johdin on valmistettu, on oma ominaisvastus.
Esimerkiksi kuparin resistanssi on 0,017, eli kuparilangan, jonka pituus on 1 m ja poikkileikkaus 1 mm2, resistanssi on 0,017 ohmia. Alumiinin vastus on 0,03, raudan vastus on 0,12, konstantaanin vastus on 0,48 ja nikromin vastus on 1-1,1.
Lue aiheesta lisää täältä: Mikä on sähkövastus?
Johdon vastus on suoraan verrannollinen sen pituuteen, eli mitä pidempi lanka, sitä suurempi sen sähkövastus.
Johdon vastus on kääntäen verrannollinen sen poikkileikkauspinta-alaan, eli mitä paksumpi lanka, sitä pienempi sen vastus, ja päinvastoin, mitä ohuempi lanka, sitä suurempi sen vastus.
Ymmärtääksesi paremmin tätä suhdetta, kuvittele kaksi paria kommunikoivia suonia, joista toisessa on ohut liitosputki ja toisessa paksu. On selvää, että kun yksi astioista (jokainen pari) täytetään vedellä, sen siirto toiseen astiaan paksun putken läpi tapahtuu paljon nopeammin kuin ohuen, ts. paksu putki vastustaa vähemmän vettä. Samoin sähkövirran on helpompi kulkea paksun johdon läpi kuin ohuen, eli ensimmäisellä on vähemmän vastusta kuin jälkimmäisellä.
Johtimen sähkövastus on yhtä suuri kuin sen materiaalin ominaisresistanssi, josta tämä johdin on valmistettu, kerrottuna johtimen pituudella ja jaettuna johtimen poikkileikkausalan pinta-alalla. kapellimestari:
R = p l / S,
missä — R — langan vastus, ohm, l — pituus johdossa metreinä, C — langan poikkileikkausala, mm2.
Pyöreän langan poikkileikkausala laskettuna kaavalla:
S = Pi xd2/4
jossa Pi on vakioarvo, joka on yhtä suuri kuin 3,14; d - langan halkaisija.
Ja näin langan pituus määritetään:
l = S R / p,
Tämän kaavan avulla on mahdollista määrittää langan pituus, poikkileikkaus ja vastus, jos muut kaavaan sisältyvät suureet tunnetaan.
Jos on tarpeen määrittää langan poikkipinta-ala, kaava johtaa seuraavaan muotoon:
S = p l / R
Muuntamalla samaa kaavaa ja ratkaisemalla yhtälön p:llä, löydämme langan resistanssin:
R = R S/l
Jälkimmäistä kaavaa tulee käyttää tapauksissa, joissa johtimen vastus ja mitat ovat tiedossa, mutta sen materiaalia ei tunneta, ja lisäksi sitä on vaikea määrittää sen ulkonäön perusteella. Tätä varten on tarpeen määrittää langan vastus ja löytää taulukon avulla materiaali, jolla on tällainen vastus.

Toinen johtojen resistanssiin vaikuttava tekijä on lämpötila.
On todettu, että lämpötilan noustessa metallilankojen vastus kasvaa ja pienentyessä se pienenee. Tämä puhtaiden metallijohtimien resistanssin lisäys tai lasku on lähes sama ja keskimäärin 0,4 % 1 °C:ssa... Nestejohtimien ja hiilen resistanssi pienenee lämpötilan noustessa.
 Aineen rakenteen elektroninen teoria antaa seuraavan selityksen metallijohtimien resistanssin kasvulle lämpötilan noustessa.Kuumennettaessa johdin saa lämpöenergiaa, joka välittyy väistämättä kaikkiin aineen atomeihin, minkä seurauksena niiden liikkeen intensiteetti kasvaa. Atomien lisääntynyt liike luo suuremman vastuksen vapaiden elektronien suunnatulle liikkeelle, minkä vuoksi johtimen vastus kasvaa. Lämpötilan laskiessa syntyy paremmat olosuhteet elektronien suuntautuneelle liikkeelle ja johtimen vastus pienenee. Tämä selittää mielenkiintoisen ilmiön - metallien suprajohtavuuden.
Aineen rakenteen elektroninen teoria antaa seuraavan selityksen metallijohtimien resistanssin kasvulle lämpötilan noustessa.Kuumennettaessa johdin saa lämpöenergiaa, joka välittyy väistämättä kaikkiin aineen atomeihin, minkä seurauksena niiden liikkeen intensiteetti kasvaa. Atomien lisääntynyt liike luo suuremman vastuksen vapaiden elektronien suunnatulle liikkeelle, minkä vuoksi johtimen vastus kasvaa. Lämpötilan laskiessa syntyy paremmat olosuhteet elektronien suuntautuneelle liikkeelle ja johtimen vastus pienenee. Tämä selittää mielenkiintoisen ilmiön - metallien suprajohtavuuden.
Suprajohtavuus Metallien resistanssin pieneneminen nollaan tapahtuu valtavassa negatiivisessa lämpötilassa -273° ° Ns. absoluuttinen nolla. Absoluuttisen nollan lämpötilassa metalliatomit näyttävät jäätyvän paikoilleen täysin häiriintymättä elektronien liikkeestä.
