Aktiivinen vastus ja kela AC-piirissä

Ottaen huomioon vaihtovirtapiirin, joka sisältää vain induktiivisen vastuksen (katso artikkeli "Induktori vaihtovirtapiirissä"), oletimme, että tämän piirin aktiivinen vastus on nolla.

Itse asiassa sekä itse kelan johdolla että liitäntäjohtimilla on pieni mutta aktiivinen vastus, joten piiri kuluttaa väistämättä virtalähteen energiaa.

Siksi ulkoisen piirin kokonaisresistanssia määritettäessä on tarpeen lisätä sen reaktiivinen ja aktiivinen vastus. Mutta on mahdotonta lisätä näitä kahta vastustusta, jotka ovat luonteeltaan erilaisia.

Tässä tapauksessa piirin impedanssi vaihtovirtaan löydetään geometrisella summauksella.

Muodostetaan suorakulmainen kolmio (katso kuva 1), jonka toinen puoli on induktiivisen resistanssin arvo ja toinen puoli aktiivisen vastuksen arvo. Haluttu piiriimpedanssi määräytyy kolmion kolmannen sivun mukaan.

Kuva 1. Induktiivisen ja aktiivisen resistanssin sisältävän piirin impedanssin määritys

Piirin impedanssi on merkitty latinalaisella kirjaimella Z ja mitataan ohmeina. Rakenteesta voidaan nähdä, että kokonaisvastus on aina suurempi kuin induktiivinen ja aktiivinen vastus erikseen otettuna.

Piirin kokonaisresistanssin algebrallinen lauseke on:

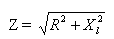
missä Z — kokonaisvastus, R — aktiivinen vastus, XL — piirin induktiivinen vastus.

Siksi aktiivisesta ja induktiivisesta resistanssista koostuvan piirin kokonaisvastus vaihtovirralle on yhtä suuri kuin tämän piirin aktiivisen ja induktiivisen resistanssin neliösumman neliöjuuri.

Ohmin laki koska tällainen piiri ilmaistaan ​​kaavalla I = U / Z, missä Z on piirin kokonaisresistanssi.

Analysoidaan nyt mikä jännite tulee olemaan, jos piirillä on virran ja induktanssin välisen vaihesiirron ja lisäksi suhteellisen suuri aktiivinen vastus. Käytännössä tällainen piiri voi olla esimerkiksi piiri, joka sisältää ohuella langalla kierretyn rautasydämisen kelan (korkeataajuinen kuristin).

Tässä tapauksessa vaihesiirto virran ja jännitteen välillä ei ole enää neljännesjaksoa (kuten se oli piirissä, jossa on vain induktiivinen vastus), vaan paljon pienempi; ja mitä suurempi vastus, sitä vähemmän vaihesiirtoa syntyy.

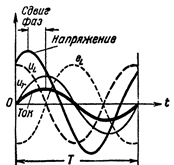
Kuva 2. Virta ja jännite piirissä, joka sisältää R:n ja L:n.

Nyt hän itse Itseinduktion EMF ei ole vastavaiheessa virtalähdejännitteen kanssa, koska se ei ole jännitteen suhteen poikkeamassa puolella jaksolla, vaan vähemmän.Lisäksi kelan napoihin virtalähteen luoma jännite ei ole yhtä suuri kuin itseinduktion emf, vaan se on suurempi kuin kelajohtimen aktiivisen resistanssin jännitehäviön määrä. Toisin sanoen kelan jännite koostuu joka tapauksessa kahdesta komponentista:

• tiL- jännitteen reaktiivinen komponentti, joka tasapainottaa itseinduktion EMF:n vaikutusta,

• tiR- jännitteen aktiivinen komponentti, joka voittaa piirin aktiivisen vastuksen.

Jos käämin kanssa kytketään sarjaan suuri aktiivinen vastus, vaihesiirtymä pienenee niin paljon, että virran siniaalto lähes saavuttaa jännitteen siniaallon ja niiden välinen vaiheero on tuskin havaittavissa. termin amplitudi ja on suurempi kuin termin amplitudi.

Vastaavasti voit pienentää vaihesiirtoa ja jopa kokonaan nollaa, jos pienennät generaattorin taajuutta jollain tavalla. Taajuuden lasku johtaa itseinduktio-EMF:n vähenemiseen ja siten sen aiheuttaman virran ja jännitteen välisen vaihesiirron vähenemiseen.

Induktorin sisältävän vaihtovirtapiirin teho

Käämin sisältävä vaihtovirtapiiri ei kuluta virtalähteen energiaa ja että piirissä tapahtuu energianvaihtoprosessi generaattorin ja piirin välillä.

Analysoidaan nyt, kuinka asiat ovat tällaisen järjestelmän kuluttaman tehon kanssa.

Vaihtovirtapiirissä kulutettu teho on yhtä suuri kuin virran ja jännitteen tulo, mutta koska virta ja jännite ovat muuttuvia määriä, myös teho on muuttuva.Tässä tapauksessa voimme määrittää kullekin ajanhetkelle tehoarvon, jos kerromme nykyisen arvon tiettyä ajanhetkeä vastaavalla jännitearvolla.

Tehokaavion saamiseksi meidän on kerrottava suorien segmenttien arvot, jotka määrittävät virran ja jännitteen eri aikoina. Tällainen rakenne on esitetty kuvassa. 3, a. Katkoviiva aaltomuoto p näyttää meille, kuinka teho muuttuu vaihtovirtapiirissä, joka sisältää vain induktiivisen vastuksen.

Tämän käyrän muodostamisessa käytettiin seuraavaa algebrallista kertolaskua: Kun positiivinen arvo kerrotaan negatiivisella arvolla, saadaan negatiivinen arvo ja kun kaksi negatiivista tai kaksi positiivista arvoa kerrotaan, saadaan positiivinen arvo.

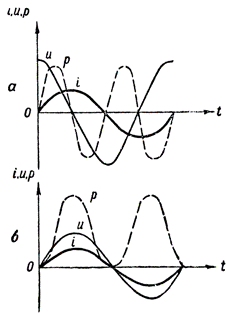
Kuva 3. Tehokäyrät: a — induktiivisen vastuksen sisältävässä piirissä, b — myös aktiivinen vastus

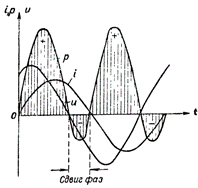
Kuva 4. Tehokäyrä R:n ja L:n sisältävälle piirille.

Tehokäyrä on tässä tapauksessa aika-akselin yläpuolella. Tämä tarkoittaa, että generaattorin ja piirin välillä ei tapahdu energianvaihtoa ja siksi generaattorin piiriin syöttämä teho kuluu kokonaan piirissä.

Kuvassa Kuva 4 esittää tehokäyrän piirille, joka sisältää sekä induktiivisen että aktiivisen vastuksen. Tässä tapauksessa tapahtuu myös käänteinen energian siirto piiristä virtalähteeseen, mutta paljon vähemmässä määrin kuin piirissä, jossa on yksi induktiivinen vastus.

Yllä olevien tehokaavioiden tarkastelun jälkeen päättelemme, että vain vaihesiirto virran ja jännitteen välillä piirissä luo "negatiivisen" tehon.Tässä tapauksessa mitä suurempi vaihesiirto virran ja jännitteen välillä piirissä, sitä vähemmän virtaa piiri kuluttaa, ja päinvastoin, mitä pienempi vaihesiirto, sitä suurempi virtapiiri kuluttaa.

Lue myös: Mikä on jänniteresonanssi