Mikä on sisäinen vastus

Oletetaan, että on olemassa yksinkertainen sähköinen suljettu piiri, joka sisältää virtalähteen, esimerkiksi generaattorin, galvaanisen kennon tai akun, ja vastuksen R. Koska virtapiirissä ei ole katkaistua missään, se kulkee myös lähteen sisällä.

Tällaisessa tilanteessa voimme sanoa, että jokaisella lähteellä on sisäinen vastus, joka estää virran kulkemisen. Tämä sisäinen vastus luonnehtii virtalähdettä ja on merkitty kirjaimella r. varten galvaaninen kenno tai akku, sisäinen vastus on elektrolyyttiliuoksen ja elektrodien resistanssi, generaattorilla - staattorikäämien resistanssi jne.

Siten virtalähteelle on tunnusomaista sekä EMF:n suuruus että sen oman sisäisen vastuksen arvo r - molemmat ominaisuudet osoittavat lähteen laadun.

Korkeajännitteisissä sähköstaattisissa generaattoreissa (kuten Van de Graaf- tai Wimshurst-generaattorissa) on valtava EMF, joka mitataan miljoonissa voltteissa, kun taas niiden sisäinen resistanssi mitataan sadoissa megaohmeissa, joten ne eivät sovellu korkeat virrat.

Päinvastoin galvaanisten kennojen (kuten akun) EMF on luokkaa 1 voltti, vaikka niiden sisäinen vastus on murto-osien tai enintään kymmenen ohmin luokkaa, ja siksi voidaan saada yksiköiden ja kymmenien ampeerien virtoja. galvaanisista kennoista.

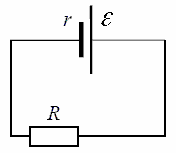
Tämä kaavio näyttää todellisen lähteen, johon on kytketty kuorma. Ne määritellään tässä EMF lähde, sen sisäinen vastus sekä kuormituskestävyys. Mukaan Ohmin laki suljetulle piirille, tämän piirin virta on yhtä suuri:

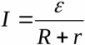
Koska ulkoisen piirin osa on homogeeninen, Ohmin laista voidaan löytää jännite kuorman yli:

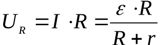
Ilmaisemalla kuorman resistanssin ensimmäisestä yhtälöstä ja korvaamalla sen arvon toiseen yhtälöön, saamme kuorman jännitteen riippuvuuden virrasta suljetussa piirissä:

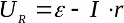
Suljetussa silmukassa EMF on yhtä suuri kuin ulkoisten piirielementtien ja itse lähteen sisäisen resistanssin jännitehäviön summa. Kuormajännitteen riippuvuus kuormitusvirrasta on ihanteellisesti lineaarinen.

Kaavio näyttää tämän, mutta todellisen vastuksen kokeelliset tiedot (ristit lähellä kuvaajaa) eroavat aina ihanteellisesta:

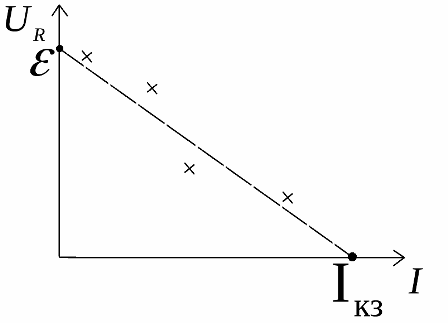
Kokeet ja logiikka osoittavat, että nollakuormitusvirralla ulkoisen piirin jännite on yhtä suuri kuin lähteen emf ja nollakuormitusjännitteellä piirivirta on oikosulkuvirta… Tämä todellisten piirien ominaisuus auttaa löytämään kokeellisesti todellisten lähteiden EMF:n ja sisäisen resistanssin.

Sisäisen vastuksen kokeellinen havaitseminen

Näiden ominaisuuksien kokeellisen määrittämiseksi rakennetaan kaavio kuorman jännitteen riippuvuudesta virran suuruudesta, minkä jälkeen se ekstrapoloidaan akselien leikkauspisteeseen.

Kuvaajan leikkauspisteessä jännitepään kanssa on lähteen emf:n arvo ja virran akselin leikkauspisteessä oikosulkuvirran arvo. Tämän seurauksena sisäinen vastus saadaan kaavasta:

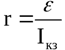
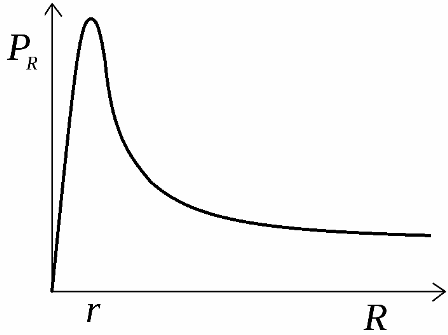
Lähteen kehittämä hyötyteho jakautuu kuormaan. Kaavio tämän tehon riippuvuudesta kuormitusvastukseen on esitetty kuvassa. Tämä käyrä alkaa koordinaattiakselien leikkauspisteestä nollapisteessä, nousee sitten maksimitehoarvoon ja putoaa sitten nollaan, kun kuormitusvastus on yhtä suuri kuin ääretön.

Jotta saadaan selville suurin kuormitusvastus, jolla teoreettinen maksimiteho kehittyy tietyllä lähteellä, otetaan tehokaavan derivaatta suhteessa R:ään ja asetetaan se nollaan. Maksimiteho kehittyy, kun ulkoisen piirin resistanssi on yhtä suuri kuin sisäisen lähteen resistanssi:

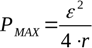
Tämä enimmäistehoa koskeva säännös R = r mahdollistaa lähteen sisäisen resistanssin kokeellisen selvittämisen piirtämällä kuormalla vapautuvan tehon kuormitusvastuksen arvon funktiona.Teholähteen todellisen sisäisen resistanssin määrittäminen todellisen eikä teoreettisen kuormitusvastuksen, joka antaa maksimaalisen tehon, löytäminen.

Virtalähteen hyötysuhde ilmaisee kuormaan jaetun maksimitehon suhteen parhaillaan kehitteillä olevaan kokonaistehoon

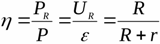
On selvää, että jos lähde kehittää sellaisen tehon, että kuormituksella saavutetaan suurin mahdollinen teho tietylle lähteelle, lähteen hyötysuhde on 50%.