Ohmin laki magneettiselle piirille

Jos magneettivuoja ei olisi, on epätodennäköistä, että modernia sähkötekniikkaa olisi olemassa. Generaattorien ja sähkömoottoreiden, sähkömagneettien ja muuntajien, mittauslaitteiden ja Hall-anturien toiminta perustuu magneettikentän käyttöön ja magneettivuon ominaisuuksiin.

Magneettivuon keskittämiseksi ja vahvistamiseksi he turvautuvat ferromagneettisten materiaalien käyttöön. Ferromagneettisia materiaaleja valmistetaan magneettiset ytimet — vaaditun muotoiset ja -kokoiset kappaleet, ytimet yhden tai toisen kokoisten magneettivuojen ohjaamiseksi vaadittuun suuntaan. Tällaisia ​​kappaleita, joiden sisällä kulkevat suljetut magneettisen induktion linjat, kutsutaan magneettipiireiksi.

Magneettikentän tunnetut ominaisuudet mahdollistavat magneettivuon laskemisen eri magneettipiireissä. Mutta käytännön työssä on paljon kätevämpää turvautua yleisiin seurauksiin ja magneettipiirien lakeihin, jotka on johdettu magneettikentän laeista, sen sijaan, että käytettäisiin näitä lakeja suoraan joka kerta. Tiettyjen sääntöjen soveltaminen magneettipiireihin on kätevämpää tyypillisten käytännön ongelmien ratkaisemiseksi.

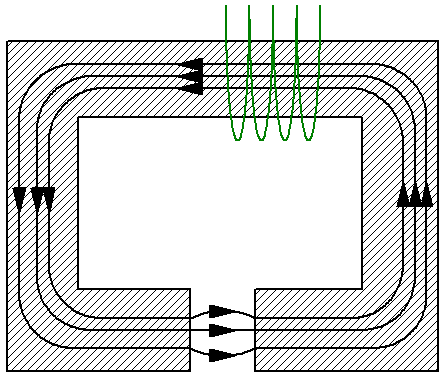
Tarkastellaan esimerkiksi yksinkertaista magneettipiiriä, joka koostuu poikkileikkaukseltaan S haaroittamattomasta ikeestä, joka puolestaan ​​on valmistettu materiaalista, jossa on läpäisevyys mu… Ikeessä on saman alueen S ei-magneettinen rako, esimerkiksi ilma, ja raon magneettinen permeabiliteetti — mu1 — on erilainen kuin ikeen magneettinen permeabiliteetti. Tässä voit katsoa induktion keskiviivaa ja soveltaa siihen magneettisen jännityksen lausetta:

Koska magneettisen induktion linjat ovat jatkuvia läpi piirin, magneettivuon suuruus sekä ikeessä että raossa on sama. Nyt käytämme kaavoja magneettinen induktio B ja magneettivuon F ilmaisemaan magneettikentän voimakkuutta H magneettivuona F.

Seuraava vaihe on korvata saadut lausekkeet yllä olevaan magneettivuolauseen kaavaan:

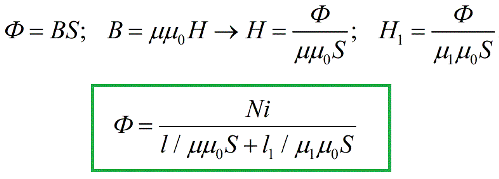
Saimme kaavan, joka on hyvin samanlainen kuin sähkötekniikassa tunnettu Ohmin laki suljetun piirin osalle, ja EMF:n rooli tässä on suurella iN, jota kutsutaan magnetomotoriseksi voimaksi (tai MDF:ksi) analogisesti sähkömotorisen voiman kanssa. SI-järjestelmässä magnetomotorinen voima mitataan ampeereina.

Nimittäjässä oleva summa ei ole muuta kuin analogia sähköpiirin kokonaissähkövastukseen, ja magneettipiirissä sitä kutsutaan vastaavasti kokonaismagneettiresistanssiksi. Nimittäjässä olevat termit ovat magneettipiirin yksittäisten osien magneettiresistanssit.

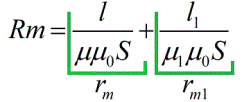
Magneettiset vastukset riippuvat magneettipiirin pituudesta, sen poikkileikkausalasta ja magneettisesta läpäisevyydestä (samanlainen kuin sähkönjohtavuus tavallisessa Ohmin laissa).Tämän seurauksena voit kirjoittaa Ohmin lain kaavan vain magneettipiirille:

Eli Ohmin lain muotoilu suhteessa magneettiseen piiriin kuulostaa tältä: "Haaroittamattomassa magneettipiirissä magneettivuo on yhtä suuri kuin MDS:n jaon osamäärä piirin kokonaismagneettiresistanssilla."

Kaavoista on selvää, että magneettinen vastus NE mitataan weber-ampeereina, ja magneettipiirin kokonaismagneettivastus on numeerisesti yhtä suuri kuin kyseisen magneettipiirin osien magneettiresistanssien summa.

Kuvattu tilanne pätee haaroittamattomalle magneettipiirille, joka sisältää minkä tahansa määrän osia, edellyttäen, että magneettivuo tunkeutuu peräkkäin kaikkiin näihin osiin. Jos magneettisydämet on kytketty sarjaan, niin kokonaismagneettiresistanssi saadaan laskemalla yhteen osien magneettivastukset.

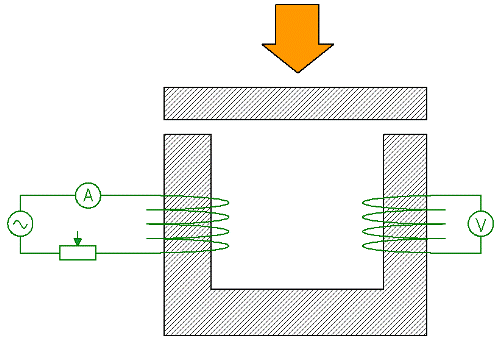
Tarkastellaan nyt koetta, joka osoittaa piirin osien reluktanssin vaikutuksen piirin kokonaisreluktanssiin.U:n muotoinen magneettipiiri magnetoidaan kelalla 1, joka syötetään (vaihtovirta) ampeerimittarin ja reostaatin kautta. Toisiokäämiin 2 indusoituu EMF, ja käämiin kytketyn volttimittarin lukemat, kuten tiedät, ovat verrannollisia magneettipiirin magneettivuon.

Jos nyt pidät ensiökäämin virran muuttumattomana säätämällä sitä reostaatilla ja painat samalla rautalevyä yllä olevaa magneettipiiriä vasten, sen jälkeen kun piirin kokonaismagneettiresistanssi pienenee huomattavasti, volttimittari kasvaa vastaavasti.

Tietenkin yllä olevat termit, kuten "magnetoresistanssi" ja "magnetomotorinen voima", ovat muodollisia käsitteitä, koska mikään magneettivuossa ei liiku, ei ole liikkuvia hiukkasia, se on vain visuaalinen esitys (kuten nestevirtausmalli) Lakien ymmärtäminen paremmin...

Yllä olevan kokeen ja muiden vastaavien kokeiden fyysinen tarkoitus on ymmärtää, kuinka ei-magneettisten rakojen ja magneettisten materiaalien lisääminen magneettipiiriin vaikuttaa magneettivirtaan magneettipiirissä.

Viemällä magneettipiiriin esimerkiksi magneetin lisäämme piirissä jo oleviin kappaleisiin molekyylivirtoja, jotka tuovat lisää magneettivuuksia. Muodolliset käsitteet, kuten "magneettinen vastus" ja "magnetomotorinen voima", osoittautuvat erittäin käteviksi käytännön ongelman ratkaisemisessa, minkä vuoksi niitä käytetään menestyksekkäästi sähkötekniikassa.