Kuinka laskea induktanssi
Aivan kuten kappale, jolla on massa mekaniikassa, vastustaa kiihtyvyyttä avaruudessa, mikä ilmentää inertiaa, niin induktanssi estää johtimen virtaa muuttumasta, mikä ilmentää itseinduktio-EMF:ää. Tämä on itseinduktion EMF, joka vastustaa sekä virran pienenemistä yrittäessään ylläpitää sitä että virran lisääntymistä yrittäen vähentää sitä.
Tosiasia on, että piirin virran muuttamisen (lisäyksen tai pienentämisen) aikana tämän virran luoma magneettivuo muuttuu myös, joka on paikallinen pääasiassa tämän piirin rajoittamalle alueelle. Ja kun magneettivuo kasvaa tai pienenee, se indusoi itseinduktion EMF:n (Lenzin säännön mukaan - sen aiheuttavaa syytä vastaan, eli alussa mainittua virtaa vastaan), kaikki samassa piirissä. Induktanssia L kutsutaan tässä suhteellisuustekijäksi virran I ja kokonaismagneettivuon Φ välillä, tämän virran muodostaa:
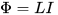
Joten mitä suurempi piirin induktanssi on, sitä vahvempi se on kuin tuloksena oleva magneettikenttä, se estää virtaa muuttumasta (se on kenttä, joka luo sen) ja siksi kestää kauemmin, ennen kuin virta muuttuu suuremman induktanssin kautta, samalla jännitteellä. Myös seuraava väite pitää paikkansa: mitä suurempi induktanssi on, sitä suurempi on jännite piirin yli, kun sen läpi kulkeva magneettivuo muuttuu.

Oletetaan, että muutamme magneettivuon tietyllä alueella vakionopeudella, niin peittämällä tämä alue eri piireillä, saamme enemmän jännitettä siihen piiriin, jonka induktanssi on suurempi (muuntaja, Rumkorf-kela jne. toimii tällä periaatteella).
Mutta miten silmukan induktanssi lasketaan? Kuinka löytää suhteellisuustekijä virran ja magneettivuon välillä? Ensimmäinen asia on muistaa, että induktanssi muuttuu henryssä (H). Piirin, jonka induktanssi on 1 henry, liittimissä, jos sen virta muuttuu yhdellä ampeerilla sekunnissa, ilmestyy 1 voltin jännite.
Induktanssin suuruus riippuu kahdesta parametrista: piirin geometrisista mitoista (pituus, leveys, kierrosten lukumäärä jne.) ja väliaineen magneettisista ominaisuuksista (jos esim. ferriittisydän on sisällä). kela, sen induktanssi on suurempi kuin jos sisällä ei ole sydäntä).
Tuotetun induktanssin laskemiseksi on tiedettävä, minkä muotoinen itse kela tulee olemaan ja mikä magneettinen permeabiliteetti sen sisällä olevalla väliaineella on (väliaineen suhteellinen magneettinen permeabiliteetti on tyhjön magneettisen permeabiliteetin ja magneettisen permeabiliteetin suhteellinen tekijä tietyn väliaineen läpäisevyys.Tietenkin se on erilainen eri materiaaleille)…
Katsotaanpa kaavoja yleisimpien kelamuotojen (sylinterinen solenoidi, toroidi ja pitkä lanka) induktanssin laskentaan.
Tässä on kaava induktanssin laskemiseksi solenoidi — kelat, joiden pituus on paljon suurempi kuin halkaisija:
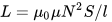
Kuten näette, tietäen kierrosten lukumäärän N, käämin pituuden l ja kelan S poikkipinta-alan, löydämme kelan likimääräisen induktanssin ilman sydäntä tai sydämen kanssa, kun taas magneettinen tyhjiön läpäisevyys on vakioarvo:
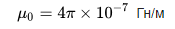
Toroidikäämin induktanssi, jossa h on toroidin korkeus, r on toroidin sisähalkaisija, R on toroidin ulkohalkaisija:
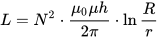
Ohuen langan induktanssi (poikkileikkauksen säde on paljon pienempi kuin pituus), jossa l on langan pituus ja r on sen poikkileikkauksen säde. Mu indekseillä i ja e ovat sisäisen (sisäiset, johdinmateriaalit) ja ulkoisen (ulkoiset, johtimen ulkopuoliset materiaalit) ympäristön suhteelliset magneettiset läpäisevyydet:
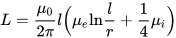
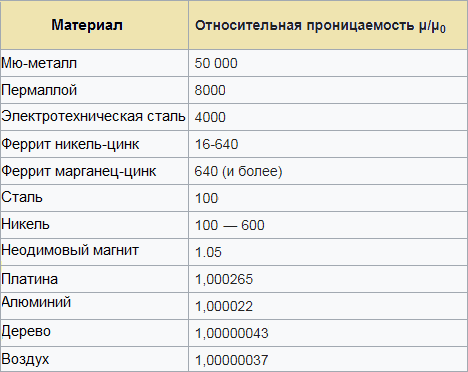
Suhteellisten permittiivisyyksien taulukko auttaa sinua arvioimaan, mitä induktanssia voit odottaa piiriltä (johdin, kela), joka käyttää tiettyä magneettista materiaalia sydämenä: