Sähkömagneettiset värähtelyt – ilman vaimennusta ja pakotettua tärinää

Induktorista ja kondensaattorista koostuvan piirin sähkömagneettiset värähtelyt johtuvat sähköenergian jaksoittaisesta muuntamisesta magneettienergiaksi ja päinvastoin. Tässä tapauksessa kondensaattorin levyjen sähkövaraus ja käämin läpi kulkevan virran suuruus muuttuvat ajoittain.

Sähkömagneettiset värähtelyt ovat vapaita ja pakotettuja. Vapaat värähtelyt vaimentuvat pääsääntöisesti nollasta poikkeavan silmukan resistanssin vuoksi, ja pakotetut värähtelyt ovat yleensä itsevärähtelyjä.

Hankkia värähtelevässä piirissä vapaita värähtelyjä, meidän on ensin saatava tämä järjestelmä pois tasapainosta: ilmoittaa kondensaattorille alkulatauksella q0 tai jollakin tavalla käynnistää virtapulssi I0 kelan läpi.

Tämä toimii eräänlaisena impulssina ja piirissä tapahtuu vapaita sähkömagneettisia värähtelyjä - alkaa kondensaattorin vuorotteleva lataus ja purkaus induktiivisen kelan kautta ja vastaavasti kelan magneettikentän muuttuva nousu ja lasku.

Värähtelyjä, joita piirissä ylläpitää ulkoinen vaihtuva sähkömotorinen voima, kutsutaan pakotetuiksi värähtelyiksi. Joten, kuten jo ymmärsit, esimerkki yksinkertaisimmasta värähtelyjärjestelmästä, jossa vapaita sähkömagneettisia värähtelyjä voidaan havaita, on värähtelypiiri, joka koostuu kondensaattorista, jonka sähkökapasiteetti on C, ja kelasta, jonka induktanssi on L.

Todellisessa värähtelypiirissä kondensaattorin latausprosessi toistetaan ajoittain, mutta värähtelyt kuolevat nopeasti, koska energiaa haihtuu pääasiassa kelajohtimen aktiivivastukseen R.

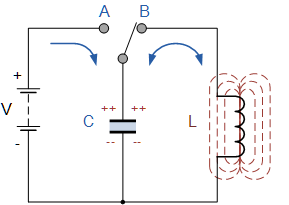
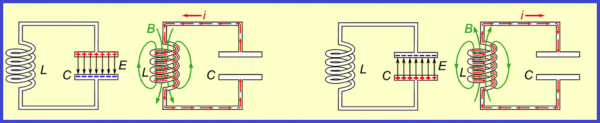
Harkitse piiriä, jossa on ihanteellinen värähtelypiiri. Lataakaamme ensin kondensaattori akusta - annamme sille alkulatauksen q0, eli täytämme kondensaattorin energialla. Tämä on kondensaattorin We suurin energia.

Seuraava vaihe on irrottaa kondensaattori akusta ja kytkeä se rinnan induktorin kanssa. Tässä vaiheessa kondensaattori alkaa purkautua ja kelapiiriin ilmestyy kasvava virta. Mitä pidempään kondensaattori purkautuu, sitä enemmän varausta siitä vähitellen siirtyy käämiin, sitä suuremmaksi käämin virta tulee, jolloin käämi varastoi energiaa magneettikentän muodossa.

Tämä prosessi ei tapahdu hetkessä, vaan asteittain, koska kelalla on induktanssi, mikä tarkoittaa, että tapahtuu itseinduktioilmiö, joka koostuu siitä, että käämi joka tapauksessa vastustaa virran kasvua. Jossain vaiheessa kelan magneettikentän energia saavuttaa suurimman mahdollisen arvon Wm (riippuen siitä, kuinka paljon varausta alun perin siirrettiin kondensaattoriin ja mikä on piirin vastus).

Myös itseinduktioilmiön vuoksi kelan läpi kulkeva virta pysyy samassa suunnassa, mutta sen suuruus pienenee ja sähkövaraus kerääntyy lopulta uudelleen kondensaattoriin. Tällä tavalla kondensaattori latautuu. Sen levyissä on nyt päinvastaiset varausmerkit kuin kokeen alussa, kun liitimme kondensaattorin akkuun.

Kondensaattorin energia on saavuttanut suurimman mahdollisen arvon tälle piirille. Virta virtapiirissä on pysähtynyt. Nyt prosessi alkaa mennä päinvastaiseen suuntaan ja tämä jatkuu yhä uudelleen, eli tulee vapaita sähkömagneettisia värähtelyjä.

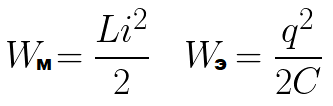
Jos piirin R aktiivinen resistanssi on yhtä suuri kuin nolla, niin kondensaattorilevyjen jännite ja kelan läpi kulkeva virta vaihtelevat äärettömästi harmonisen lain - kosinin tai sinin - mukaan. Tätä kutsutaan harmoniseksi värähtelyksi. Myös kondensaattorilevyjen varaus muuttuisi harmonisen lain mukaan.

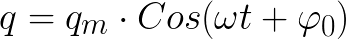
Ihanteellisessa syklissä ei ole tappiota. Ja jos olisi, vapaan värähtelyn jakso piirissä riippuisi vain kondensaattorin kapasitanssin C arvosta ja käämin induktanssista L. Tämä jakso voidaan löytää (ihanteelliselle silmukalle, jossa R = 0) käyttämällä Thomsonin kaavaa:

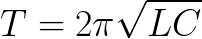
Ihanteelliselle häviöttömälle piirille löydetään vastaava taajuus ja syklitaajuus seuraavilla kaavoilla:

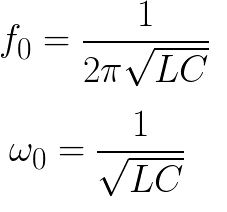
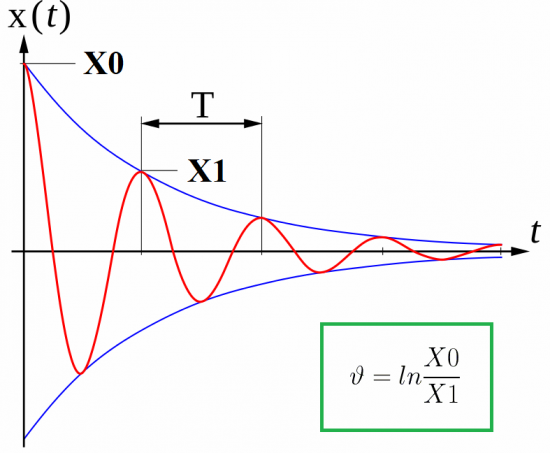
Mutta ihanteellisia piirejä ei ole olemassa, ja sähkömagneettiset värähtelyt vaimentuvat johtimien kuumenemisesta johtuvista häviöistä. Piirin resistanssin R arvosta riippuen jokainen seuraava maksimikondensaattorijännite on pienempi kuin edellinen.

Tämän ilmiön yhteydessä fysiikassa otetaan käyttöön sellainen parametri kuin värähtelyjen logaritminen dekrementti tai vaimennusvähennys. Se löytyy luonnollisena logaritmina värähtelyjen kahden peräkkäisen maksimin (saman merkin) suhteen:

Logaritminen värähtelyvähennys liittyy ihanteelliseen värähtelyjaksoon seuraavalla suhteella, jossa voidaan ottaa käyttöön lisäparametri, ns. Vaimennuskerroin:

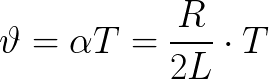
Vaimennus vaikuttaa vapaan värähtelyn taajuuteen. Siksi kaava vapaiden vaimennettujen värähtelyjen taajuuden löytämiseksi todellisessa värähtelypiirissä eroaa ihanteellisen piirin kaavasta (vaimennuskerroin otetaan huomioon):

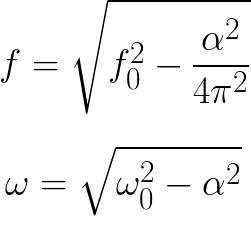
Tehdä värähtelyjä piirissä mykistetty, on tarpeen täydentää ja kompensoida nämä tappiot puolivälin välein. Tämä saavutetaan jatkuvassa värähtelygeneraattoreissa, joissa ulkoinen EMF-lähde kompensoi lämpöhäviöt energiallaan. Tällaista värähtelyjärjestelmää ulkoisen EMF-lähteen kanssa kutsutaan itsevärähteleväksi.