Sähkökentän ominaisuudet

Artikkelissa kuvataan sähkökentän pääominaisuudet: potentiaali, jännite ja intensiteetti.

Mikä on sähkökenttä

Sähkökentän luomiseksi on tarpeen luoda sähkövaraus. Varauksia (varautuneita kappaleita) ympäröivän tilan ominaisuudet eroavat sen tilan ominaisuuksista, jossa ei ole varauksia. Samaan aikaan avaruuden ominaisuudet, kun siihen johdetaan sähkövaraus, eivät muutu hetkessä: muutos alkaa varauksesta ja leviää tietyllä nopeudella avaruuden pisteestä toiseen.

Varauksen sisältävässä tilassa ilmenee mekaanisia voimia, jotka vaikuttavat siihen tilaan tuotuihin muihin varauksiin. Nämä voimat eivät ole seurausta yhden varauksen suorasta vaikutuksesta toiseen, vaan vaikutuksesta laadullisesti muuttuneen väliaineen kautta.

Sähkövarausten ympärillä olevaa tilaa, jossa siihen tuotuihin sähkövarauksiin vaikuttavat voimat ilmenevät, kutsutaan sähkökentällä.

Sähkökentässä oleva varaus liikkuu siihen kentän sivulta vaikuttavan voiman suuntaan.Tällaisen varauksen lepotila on mahdollinen vain, kun sähkökentän voimakkuutta tasapainottavaan varaukseen kohdistetaan jokin ulkoinen (ulkoinen) voima.

Heti kun ulkoisen voiman ja kentänvoimakkuuden välinen tasapaino häiriintyy, varaus alkaa taas liikkua. Sen liikkeen suunta on aina sama kuin suuremman voiman suunta.

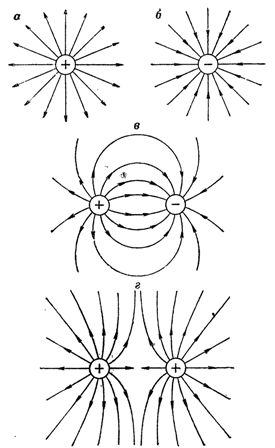
Selvyyden vuoksi sähkökenttää edustavat yleensä niin sanotut sähkökenttäviivat. Nämä viivat ovat yhtäpitäviä sähkökentässä vaikuttavien voimien suunnan kanssa. Samalla sovittiin piirrettäväksi niin monta viivaa, että niiden lukumäärä jokaista 1 cm2:tä kohti kohtisuoraan viivoja vastaan ​​asennettua pinta-alaa kohti oli verrannollinen kentän voimakkuuteen vastaavassa pisteessä.

Kentän suunnaksi pidetään yleensä tiettyyn kenttään sijoitettuun positiiviseen varaukseen vaikuttavan kentänvoimakkuuden suuntaa. Positiiviset varaukset hylkivät positiiviset varaukset ja houkuttelevat negatiiviset varaukset. Siksi kenttä on suunnattu positiivisista varauksista negatiivisiin varauksiin.

Voimalinjojen suunta on osoitettu piirustuksissa nuolilla. Tiede on osoittanut, että sähkökentän voimalinjoilla on alku ja loppu, eli ne eivät ole suljettuja itsestään. Kentän oletetun suunnan perusteella havaitaan, että voimalinjat alkavat positiivisilla varauksilla (positiivisesti varautuneilla kappaleilla) ja päättyvät negatiivisiin varauksiin.

Riisi. 1. Esimerkkejä kuvasta sähkökentästä, jossa käytetään voimalinjoja: a - sähkökenttä yhdellä positiivisella varauksella, b - sähkökenttä yhdellä negatiivisella varauksella, c - kahden vastakkaisen varauksen sähkökenttä, d - an kahden samanlaisen varauksen sähkökenttä

KuvassaKuva 1 esittää esimerkkejä sähkökentästä, joka on kuvattu voimalinjoja käyttäen. On muistettava, että sähkökenttäviivat ovat vain tapa graafisesti esittää kenttää. Tässä ei ole suurempaa sisältöä voimalinjan käsitteelle.

Coulombin laki

Kahden varauksen välisen vuorovaikutuksen voimakkuus riippuu varausten koosta ja keskinäisestä järjestelystä sekä niiden ympäristön fysikaalisista ominaisuuksista.

Kahden sähköistetyn fyysisen kappaleen osalta, joiden mitat ovat merkityksettömiä kappaleiden väliseen etäisyyteen verrattuna, vuorovaikutuksen paraneminen määritetään matemaattisesti seuraavasti:

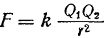
jossa F on varausten vuorovaikutusvoima newtoneina (N), k - varausten välinen etäisyys metreinä (m), Q1 ja Q2 - sähkövarausten suuruus kuloneina (k), k on suhteellisuuskerroin, jonka arvo riippuu varauksia ympäröivän väliaineen ominaisuuksista.

Yllä oleva kaava kuuluu näin: kahden pistevarauksen välinen vuorovaikutusvoima on suoraan verrannollinen näiden varausten suuruuden tuloon ja kääntäen verrannollinen niiden välisen etäisyyden neliöön (Coulombin laki).

Suhteellisuustekijän k määrittämiseksi käytä lauseketta k = 1 /(4πεεО).

Sähkökentän potentiaali

Sähkökenttä saa aina liikettä varaukselle, jos varaukseen vaikuttavia kenttävoimia ei tasapainota ulkopuolisten voimien vaikutuksesta. Tämä tarkoittaa, että sähkökentällä on potentiaalienergiaa, eli kykyä tehdä työtä.

Siirtämällä varausta avaruuden pisteestä toiseen sähkökenttä toimii, minkä seurauksena kentän potentiaalienergian syöttö vähenee.Jos varaus liikkuu sähkökentässä jonkin kenttävoimia vastapäätä toimivan ulkoisen voiman vaikutuksesta, niin työtä eivät tee sähkökenttävoimat, vaan ulkoiset voimat. Tässä tapauksessa kentän potentiaalienergia ei vain vähene, vaan päinvastoin kasvaa.

Ulkoisen voiman työ, joka siirtää varausta sähkökentässä, on verrannollinen liikettä vastustavien kenttävoimien suuruuteen. Tässä tapauksessa ulkoisten voimien tekemä työ kuluu kokonaan kentän potentiaalisen energian lisäämiseen. Kentän karakterisoimiseksi sen potentiaalienergian puolelta kutsutaan suuruutta, jota kutsutaan sähkökentän potentiaaliksi.

Tämän määrän olemus on seuraava. Oletetaan, että positiivinen varaus on tarkasteltavan sähkökentän ulkopuolella. Tämä tarkoittaa, että kentällä ei käytännössä ole vaikutusta annettuun varaukseen. Anna ulkoisen voiman viedä tämä varaus sähkökenttään ja kenttävoimien aiheuttaman liikevastuksen voittaessa siirtää varaus tiettyyn kentän pisteeseen. Voiman tekemä työ ja siten määrä, jolla kentän potentiaalienergia on kasvanut, riippuu täysin kentän ominaisuuksista. Siksi tämä työ voi karakterisoida tietyn sähkökentän energian.

Tiettyyn kentän pisteeseen sijoitettuun positiivisen varauksen yksikköön liittyvää sähkökentän energiaa kutsutaan kenttäpotentiaaliksi tietyssä pisteessä.

Jos potentiaalia merkitään kirjaimella φ, varausta kirjaimella q ja varauksen siirtämiseen käytettyä työtä W:llä, kenttäpotentiaali tietyssä pisteessä ilmaistaan ​​kaavalla φ = W / q.

Tästä seuraa, että sähkökentän potentiaali tietyssä pisteessä on numeerisesti yhtä suuri kuin ulkoisen voiman tekemä työ, kun yksikköpositiivinen varaus siirtyy pois kentästä tiettyä pistettä kohti. Kenttäpotentiaali mitataan voltteina (V). Jos yhden kulon sähköä siirrettäessä kentän ulkopuolelle tiettyyn pisteeseen ulkoiset voimat ovat tehneet yhtä joulen verran työtä, niin kentän tietyssä pisteessä potentiaali on yhtä volttia: 1 voltti = 1 joule / 1 coulomb

Sähkökentän voimakkuus

Missä tahansa sähkökentässä positiiviset varaukset siirtyvät suuremman potentiaalin kohdista pienempipotentiaalisiin pisteisiin. Päinvastoin, negatiiviset varaukset siirtyvät pienemmän potentiaalin kohdista korkeamman potentiaalin pisteisiin. Molemmissa tapauksissa työ tehdään sähkökentän potentiaalienergian kustannuksella.

Jos tiedämme tämän työn, eli määrän, jolla kentän potentiaalienergia on pienentynyt, kun positiivinen varaus q siirtyy kentän pisteestä 1 pisteeseen 2, on helppo löytää jännite näiden pisteiden välillä. kenttä U1,2:

U1,2 = A / q,

jossa A on kenttävoimien työ, kun varaus q siirretään pisteestä 1 pisteeseen 2. Sähkökentän kahden pisteen välinen jännite on numeerisesti yhtä suuri kuin nollan tekemä työ siirtääkseen yksikköpositiivisen varauksen yhdestä pisteestä kentällä toiselle.

Kuten voidaan nähdä, kentän kahden pisteen välinen jännite ja samojen pisteiden välinen potentiaaliero edustavat samaa fyysistä yksikköä… Siksi termit jännite ja potentiaaliero ovat samat. Jännite mitataan voltteina (V).

Kahden pisteen välinen jännite on yhtä volttia, jos siirrettäessä yksi coulomb sähköä kentän pisteestä toiseen kenttävoimat toimivat yhtä joulea: 1 voltti = 1 joule / 1 coulomb

Sähkökentän voimakkuus

Coulombin laista seuraa, että tietyn varauksen sähkökenttävoimakkuus, joka vaikuttaa toiseen tähän kenttään sijoitettuun varaukseen, ei ole sama kaikissa kentän pisteissä. Sähkökenttä missä tahansa pisteessä voidaan luonnehtia sen voiman suuruudella, jolla se vaikuttaa tiettyyn pisteeseen sijoitettuun yksikköpositiiviseen varaukseen.

Kun tämä arvo tiedetään, voidaan määrittää kuhunkin varaukseen Q vaikuttava voima F. Voit kirjoittaa, että F = Q x E, missä F on voima, joka vaikuttaa sähkökentän kentässä olevaan pisteeseen sijoittuvaan varaukseen Q, E on voima, joka vaikuttaa yksikön positiiviseen varaukseen, joka on sijoitettu samaan kentän kohtaan. Suuruutta E, joka on numeerisesti yhtä suuri kuin voima, jonka yksikköpositiivinen varaus kokee tietyssä kentän pisteessä, kutsutaan sähkökentän voimakkuudeksi.