Yksivaiheinen vaihtovirta

Vaihtovirran hankkiminen

Jos lankaa A pyöritetään magneetin kahden navan muodostamassa magneettivuossa myötäpäivään (kuva 1), silloin kun lanka ylittää magneettikenttäviivat, se indusoi e. d. s jonka arvon määrää lauseke

E = Blvsinα,

missä B on magneettinen induktio yksikössä T, l on langan pituus metreinä, v on langan nopeus yksikössä m/s, α — kulma, jossa lanka leikkaa magneettikenttäviivat.

Pysyvät B, I ja v tässä tapauksessa vakioina, jolloin indusoitu e. jne. c. riippuu vain kulmasta α, jossa lanka ylittää magneettikentän. Joten kohdassa 1, kun lanka liikkuu magneettikenttäviivoja pitkin, indusoidun emf:n arvo. jne. p on nolla, kun lanka siirtyy pisteeseen 3 oe. jne. v. tulee olemaan tärkein, koska johdin ylittää voimalinjat niihin nähden kohtisuorassa suunnassa, ja lopuksi esim. jne. v. saavuttaa jälleen nollan, jos johto siirretään kohtaan 5.

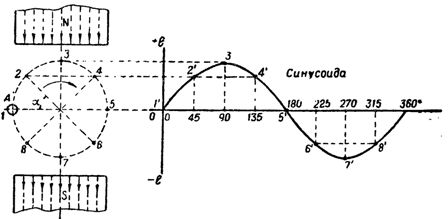
Riisi. 1. Muutetaan indusoitu e. jne. s. magneettikentässä pyörivässä johdossa

Välipisteissä 2 ja 4, joissa lanka ylittää voimalinjat kulmassa α = 45 °, indusoidun emf:n arvo. jne. c. on vastaavasti pienempi kuin kohdassa 3. Näin ollen, kun lanka käännetään pisteestä 1 pisteeseen 5, eli 180°, indusoitu e. jne. v. muuttuu nollasta maksimiin ja takaisin nollaan.

On aivan ilmeistä, että kun lankaa A käännetään edelleen 180° kulman läpi (pisteiden 6, 7, 8 ja 1 kautta), indusoidun e. jne. p. tulee olemaan sama, mutta sen suunta muuttuu päinvastaiseksi, koska lanka ylittää magneettikenttäviivat jo toisen navan alla, mikä vastaa niiden ylittämistä vastakkaiseen ensimmäiseen suuntaan.

Siksi, kun lankaa käännetään 360°, indusoitu e. jne. v. ei vain muuta suuruusluokkaansa koko ajan, vaan myös muuttaa suuntaansa kahdesti.

Jos johto on kiinni jonkin verran vastusta, lanka tulee näkyviin sähköä, myös kooltaan ja suunnaltaan vaihteleva.

Sähkövirtaa, jonka suuruus ja suunta muuttuu jatkuvasti, kutsutaan vaihtovirraksi.

Mikä on siniaalto?

Muutoksen luonne e. jne. (virta) yhden langan kierroksen osalta selkeyden vuoksi, ne on esitetty graafisesti käyrän avulla. Koska arvo e. jne. c. verrannollinen sinα:aan, jolloin tietyt kulmat on asetettu, on mahdollista taulukoiden avulla määrittää kunkin kulman sinin arvo ja sopivalla asteikolla muodostaa käyrä e:n muutokselle. jne. c. Tätä varten asetamme vaaka-akselille sivuun langan kiertokulmat ja pystyakselilla sopivassa mittakaavassa indusoitu e. jne. kanssa

Jos kuvassa 1 on aiemmin mainittu.1 yhdistä pisteet tasaisella kaarevalla viivalla, niin se antaa käsityksen indusoidun e. jne. (virta) missä tahansa johtimen kohdassa magneettikentässä. Johtuen siitä, että indusoidun e. jne. p. millä tahansa hetkellä määräytyy sen kulman sinistä, jossa lanka ylittää kuvassa 1 esitetyn magneettikentän. 1 käyrää kutsutaan sinusoidiksi, ja e. jne. s. — sinimuotoinen.

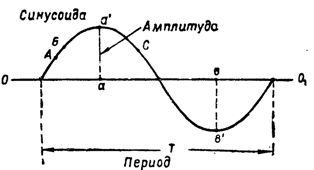
Riisi. 2. Sinimuoto ja sen ominaisarvot

Muutokset, joita tarkastelimme e. jne. c. vastaa sinimuotoisesti langan pyörimistä magneettikentässä 360°:n kulmassa. Kun lankaa käännetään seuraavat 360°, muutokset indusoituneessa e. jne. s.(ja virta) ilmestyvät jälleen siniaallona, ​​eli ne toistuvat ajoittain.

Näin ollen tämän aiheuttama e. jne. c:tä kutsutaan sähkövirran sinimuotoiseksi vaihtovirraksi... On aivan ilmeistä, että jännite, jota voimme mitata johtimen A päistä, suljetun ulkoisen piirin ollessa läsnä, muuttuu myös sinimuotoisesti.

Vaihtovirtaa, joka saadaan pyörittämällä lankaa magneettivuossa tai käämiin kytkettyä johdinjärjestelmää, kutsutaan yksivaiheiseksi vaihtovirraksi.

Sinimuotoiset vaihtovirrat ovat tekniikassa laajimmin käytettyjä. Voit kuitenkin löytää vaihtovirtoja, jotka eivät muutu sinilain mukaan. Tällaisia ​​vaihtovirtoja kutsutaan ei-sinimuotoisiksi.

Katso myös: Mikä on vaihtovirta ja miten se eroaa tasavirrasta

Yksivaiheisen vaihtovirran amplitudi, jakso, taajuus

Nykyinen vahvuus, muuttuu sinusoidia pitkin, muuttuu jatkuvasti. Joten jos pisteessä A (kuva 2) virta on yhtä suuri kuin 3a, niin kohdassa B se on jo suurempi.Jossain muussa siniaallon kohdassa, esimerkiksi pisteessä C, virralla on nyt uusi arvo ja niin edelleen.

Virran voimakkuutta tiettyinä aikoina, kun se muuttuu siniaaltoa pitkin, kutsutaan hetkellisiksi virran arvoiksi.

Yksivaiheisen vaihtovirran suurinta hetkellistä arvoa kutsutaan, kun se muuttuu sinimuotoista amplitudia pitkin... On helppo nähdä, että yhdellä langan kierrolla virta saavuttaa amplitudiarvonsa kaksi kertaa. Yksi aa:n arvoista on positiivinen ja piirretään 001-akselilta ja toinen bv' on negatiivinen ja vedetään alas akselilta.

Aika, jonka aikana indusoitu e. jne. (tai nykyinen voima) käy läpi koko muutossyklin, ns. kuukausittaisen syklin T (kuva 2). Jakso mitataan yleensä sekunneissa.

Jakson käänteislukua kutsutaan taajuudeksi (f). Toisin sanoen, vaihtovirtataajuus on jaksojen lukumäärä aikayksikköä kohti, ts. sekunneissadoo. Joten esimerkiksi jos vaihtovirta 1 sekunnin sisällä ottaa samat arvot ja suunnan kymmenen kertaa, tällaisen vaihtovirran taajuus on 10 jaksoa sekunnissa.

Taajuuden mittaamiseen käytetään jaksojen lukumäärän sijasta sekunnissa yksikköä, jota kutsutaan hertseiksi (hertseiksi). 1 hertsin taajuus vastaa taajuutta 1 lps/s. Suuria taajuuksia mitattaessa on kätevämpää käyttää 1000 kertaa hertsiä suurempaa yksikköä, ts. kilohertsiä (kHz) tai 1 000 000 kertaa hertsiä suurempi – megahertsiä (mhz).

Tekniikassa käytetyt vaihtovirrat voidaan jakaa taajuudesta riippuen matalataajuisiin virtoihin ja suurtaajuisiin virtoihin.

AC rms-arvo

Johdon läpi kulkeva tasavirta lämmittää sen. Jos käytät vaihtovirtaa johdon läpi, myös lanka kuumenee.Tämä on ymmärrettävää, sillä vaikka vaihtovirta muuttaa suuntaaan koko ajan, lämmön vapautuminen ei riipu lainkaan johdon virran suunnasta.

Kun vaihtovirta johdetaan hehkulampun läpi, sen hehkulanka hehkuu. Normaalilla 50 Hz:n vaihtovirtataajuudella valon välkkymistä ei tapahdu, koska hehkulampun hehkulangalla, jolla on lämpöinertia, ei ole aikaa jäähtyä niinä aikoina, kun virtapiirissä on nolla. Alle 50 Hz:n taajuuden vaihtovirran käyttö valaistukseen ei ole nyt toivottavaa, koska lampun intensiteetissä ilmenee epämiellyttäviä, silmiä rasittavia heilahteluja.

Jatkamalla tasavirtaanalogiaa, voimme odottaa, että johdon läpi kulkeva vaihtovirta luo sen ympärille magneettikenttä. Itse asiassa nVaihtovirta ei luo magneettikenttää, mutta koska sen luoma magneettikenttä on myös suunnaltaan ja suuruudeltaan vaihteleva.

Vaihtovirta muuttuu koko ajan sekä suuruuden että suunnan NS. Luonnollisesti herää kysymys, miten muuttuja T mitataan hyvin, ja mikä sen arvo sinimuotoa pitkin muuttuessaan pitäisi katsoa aiheuttavan tämän tai tuon toiminnan.

C Tätä tarkoitusta varten vaihtovirtaa verrataan sen tuottaman vaikutuksen suhteen tasavirtaan, jonka arvo pysyy muuttumattomana kokeen aikana.

Oletetaan, että tasavirta kulkee johdon, jonka resistanssi on vakio 10 A, läpi ja havaitaan, että lanka kuumennetaan 50 °:n lämpötilaan.Jos nyt kuljetamme saman johdon läpi ei tasavirtaa, vaan vaihtovirtaa, ja niin valitsemme sen arvon (toimien esimerkiksi reostaatilla) niin, että lanka kuumennetaan myös 50 °:n lämpötilaan, Tässä tapauksessa voidaan sanoa, että vaihtovirran vaikutus on yhtä suuri kuin tasavirran vaikutus.

Johdon lämmittäminen molemmissa tapauksissa samaan lämpötilaan osoittaa, että vaihtovirta antaa aikayksikössä johdossa saman määrän lämpöä kuin tasavirta.

Vaihtuva sinimuotoinen virta, joka lähettää tietyllä resistanssilla aikayksikköä kohden saman määrän lämpöä kuin tasavirta, joka vastaa suuruudeltaan tasavirtaa... Tätä virran arvoa kutsutaan vaihtovirran teholliseksi (Id) tai teholliseksi arvoksi. Siksi esimerkissämme vaihtovirran tehollinen arvo on 10 A... Tässä tapauksessa virran maksimiarvot (huippu) ylittävät keskimääräiset suuruusarvot.

Kokemus ja laskelmat osoittavat, että vaihtovirran teholliset arvot ovat pienempiä kuin sen amplitudiarvot √2 (1,41) kertaa. Siksi, jos virran huippuarvo tiedetään, virran Id tehollinen arvo voidaan määrittää jakamalla virran Ia amplitudi √2:lla, eli Id = Aza/√2

Toisaalta, jos virran rms-arvo tiedetään, voidaan laskea virran huippuarvo, eli Ia = Azd√2

Samat suhteet pätevät e:n amplitudille ja rms-arvoille. jne. v. ja jännitteet: Yksikkö = Ea /√2, Ud = Uа/√2

Mittalaitteet näyttävät useimmiten todelliset arvot, joten merkinnöissä indeksi «d» jätetään yleensä pois, mutta sitä ei pidä unohtaa.

Impedanssi AC-piireissä

Kun induktanssi- ja kapasitanssikuluttajat kytketään vaihtovirtapiiriin, tulee huomioida sekä aktiivisuus että reaktanssi (reaktanssi syntyy, kun kondensaattori on päällä tai kuristaa vaihtovirtapiirissä). Siksi määritettäessä tällaisen kuluttajan läpi kulkevaa virtaa on tarpeen jakaa syöttöjännite piirin (kuluttajan) impedanssilla.

Yksivaiheisen vaihtovirtapiirin impedanssi (Z) määritetään seuraavalla kaavalla:

Z = √(R2 + (ωL - 1 / ωC)2

missä R on piirin aktiivinen resistanssi ohmeina, L on piirin induktanssi henrieinä, C on piirin (kondensaattorin) kapasitanssi faradeina, ω - vaihtovirran kulmataajuus.

Vaihtovirtapiireissä käytetään erilaisia ​​kuluttajia, joissa on tarpeen ottaa huomioon joko kolme arvoa R, L, C tai vain osa niistä. Samalla on otettava huomioon vaihtovirran kulmataajuus.

Joillekin käyttäjille vain R:n ja L:n arvot voidaan ottaa huomioon vastaavilla kulmataajuusarvoilla, esimerkiksi 50 Hz:n AC-taajuudella solenoidin kela tai generaattorikäämin voidaan katsoa sisältävän vain aktiivista ja induktiivista vastusta. Toisin sanoen kapasitanssi voidaan tässä tapauksessa jättää huomiotta. Sitten tällaisen käyttäjän AC-impedanssi voidaan laskea kaavalla:

Z = √(R2 + ω2L2)

Jos tällainen kela tai vaihtovirtakäyttöön suunniteltu käämi kytketään saman jännitteen tasavirtaan, kelan läpi kulkee erittäin suuri virta, joka voi johtaa merkittävään lämmön muodostumiseen ja kelan eristys voi vaurioitua. Päinvastoin, pieni virta kulkee kelan läpi, joka on suunniteltu toimimaan tasavirtapiirissä ja kytkettynä saman jännitteen vaihtovirtapiiriin, eikä laite, jossa tätä käämiä käytetään, suorita vaadittua toimenpidettä.

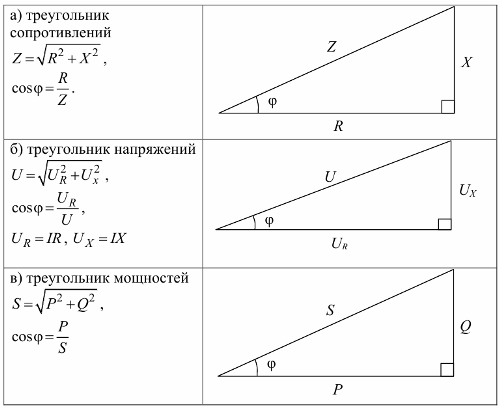
Resistanssikolmio, jännitekolmio ja tehokolmio: