Värähtelyprosessi sähkötekniikassa ja elektroniikassa, värähtelytyypit
Oskillatorinen prosessi – prosessi, jonka toistettavuus vaihtelee. Kaikki värähtelyprosessit on jaettu kahteen luokkaan: jaksollisiin ja ei-jaksollisiin. Teoriassa he käyttävät myös väliluokkaa - melkein jaksollisia värähtelyjä.
Värähtelevää prosessia kutsutaan jaksolliseksi, jossa tätä prosessia kuvaavalla arvolla, joka otetaan milloin tahansa tietyn ajanjakson T jälkeen, on sama arvo.
Funktiota f (t), joka on värähtelyprosessin matemaattinen lauseke, kutsutaan jaksolliseksi jaksolla T, jos se täyttää ehdon f (t + T) = f (t).
Jaksottaisten värähtelyprosessien luokassa päärooli on harmonisilla tai sinimuotoisilla värähtelyillä, joissa fysikaalisen suuren muutos ajan myötä tapahtuu sinin tai kosinin lain mukaan. Heidän kokonaisennätyksensä on:
y = f (t) = aCos ((2π / T) t — φ),
missä a — värähtelyjen amplitudi, φ on värähtelyn vaihe, 1 /T = f — taajuus ja 2πf = ω — syklisten tai ympyrävärähtelyjen taajuus.
Sinivärähtelyjen käyttö ja niiden ominaisuudet:
Graafisia tapoja näyttää vaihtovirta
Lähes jaksollinen funktio, joka vastaa jaksollisten värähtelyjen lukemaa, määritellään ehdolla:
| f · (t + τ) — f (t) | <= ε missä ε — anna arvo jokaiselle arvolle T.
Suuruutta τ tässä tapauksessa kutsutaan melkein jaksoksi. Jos arvo ε on hyvin pieni verrattuna f(t):n keskiarvoon hetkellä T, niin kvasijaksollinen funktio on lähellä jaksollista.
Ei-jaksolliset värähtelyt ovat paljon vaihtelevampia kuin jaksolliset. Mutta useimmiten automaatiossa joutuu kohtaamaan vaimenevia tai kasvavia sinivärähtelyjä.
Vaimennetun siniaallon lain mukaiset värähtelyt tai, kuten niitä joskus kutsutaan, vaimennetuiksi harmonisiksi värähtelyiksi, voidaan esittää yleisessä muodossa:
x = Ae-δTcos·(ω + φ),
missä t on aika, A ja φ ovat mielivaltaisia vakioita. Kasvavien harmonisten värähtelyjen lain yleinen merkintätapa eroaa vain vaimennustekijän etumerkistä δ[1 sekunti].
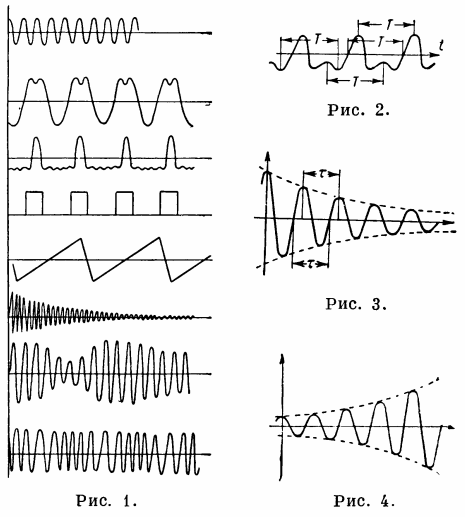
Kuva. 1 — värähtelevä prosessi, kuva. 2. — jaksollinen prosessi, kuva. 3. — vaimenevat harmoniset värähtelyt, kuva 4. — harmonisten värähtelyjen lisääntyminen.
Esimerkki värähtelyprosessin soveltamisesta on yksinkertaisin värähtelypiiri.
Oskillaattoripiiri (sähköpiiri) - passiivinen sähköpiiri, jossa voi esiintyä sähköisiä värähtelyjä taajuudella, joka määräytyy itse piirin parametrien mukaan.
Yksinkertaisin värähtelypiiri koostuu kapasitanssista C ja induktanssista L. Ulkoisen vaikutuksen puuttuessa vaimentavat värähtelyt taajuudella εО = 1/2π√LC.
Värähtelyn amplitudi pienenee esim. δT:llä, missä δ on vaimennuskerroin. Jos δ> = eO, vaimennetut värähtelyt piirissä muuttuvat ei-jaksollisiksi.
Elektroniikassa värähtelypiirin laatu määräytyy laatutekijällä: Q = nf/δ... Kun värähtelypiiriin vaikuttaa ulkoinen jaksollinen voima, syntyy siinä pakotettuja värähtelyjä. Pakotettujen värähtelyjen amplitudi kasvaa merkittävästi high-Q-piireillä, jos ulkoisen vaikutuksen taajuus on lähellä eo:ta (resonanssi). Värähtelypiiri on yksi resonanssivahvistimien pääosista, generaattorit ja muut elektroniset laitteet.
Katso myös tästä aiheesta: Jänniteresonanssin ja virtaresonanssin soveltaminen
