Perussähkösuureet: varaus, jännite, virta, teho, vastus

Perussähkösuureet: virta, jännite, vastus ja teho.

Lataus

Tärkein fysikaalinen ilmiö sähköpiireissä on liike sähkövaraus… Luonnossa on kahdenlaisia ​​varauksia – positiivisia ja negatiivisia. Kuten varaukset houkuttelevat, kuten varaukset hylkivät. Tämä johtaa siihen tosiasiaan, että on taipumus ryhmitellä positiiviset varaukset negatiivisten kanssa yhtä paljon.

Atomi koostuu positiivisesti varautuneesta ytimestä, jota ympäröi negatiivisesti varautuneiden elektronien pilvi. Negatiivinen kokonaisvaraus absoluuttisena arvona on yhtä suuri kuin ytimen positiivinen varaus. Siksi atomin kokonaisvaraus on nolla, sen sanotaan myös olevan sähköisesti neutraali.

Materiaalissa, joka kestää sähköä, jotkut elektronit ovat erotettuja atomeista ja niillä on kyky liikkua johtavassa materiaalissa. Näitä elektroneja kutsutaan liikkuviksi varauksiksi tai varauksen kantajiksi.

Koska jokainen alkutilassa oleva atomi on neutraali, negatiivisesti varautuneen elektronin erottamisen jälkeen siitä tulee positiivisesti varautunut ioni.Positiiviset ionit eivät voi liikkua vapaasti ja muodostaa kiinteiden, kiinteiden varausten järjestelmän (ks. Mitkä aineet johtavat sähköä).

Puolijohteissamuodostaen tärkeän materiaaliluokan, liikkuvat elektronit voivat liikkua kahdella tavalla: tai elektronit yksinkertaisesti käyttäytyvät negatiivisesti varautuneina kantajina. Tai monimutkainen monien elektronien kokoelma liikkuu niin kuin materiaalissa olisi positiivisesti varautuneita liikkuvia kantoaaltoja. Kiinteät maksut voivat olla luonteeltaan kumpaa tahansa.

Johtavia materiaaleja voidaan pitää materiaaleina, jotka sisältävät liikkuvia varauksenkuljettajia (joilla voi olla toinen kahdesta merkistä) ja kiinteitä varauksia, joilla on vastakkainen polariteetti.

On myös materiaaleja, joita kutsutaan eristeiksi, jotka eivät johda sähköä. Kaikki eristimen maksut ovat kiinteitä. Esimerkkejä eristeistä ovat ilma, kiille, lasi, ohuet oksidikerrokset, jotka muodostuvat monien metallien pinnoille, ja tietysti tyhjiö (jossa ei ole lainkaan varauksia).

Varaus mitataan kuloneina (C) ja sitä merkitään yleensä Q:lla.

Varauksen määrä tai negatiivisen sähkön määrä elektronia kohti on määritetty lukuisilla kokeilla ja sen on todettu olevan 1,601 × 10-19 CL tai 4,803 x 10-10 sähköstaattista varausta.

Jotain käsitystä langan läpi virtaavien elektronien määrästä jopa suhteellisen pienillä virroilla voidaan saada seuraavasti. Koska elektronin varaus on 1,601 • 10-19 CL, niin kulloin suuruisen varauksen muodostavien elektronien lukumäärä on annetun käänteisluku, eli se on suunnilleen yhtä suuri kuin 6 • 1018.

1 A:n virta vastaa 1 C:n virtausta sekunnissa, ja vain 1 μmka (10-12 A) virralla johdon poikkileikkauksen läpi noin 6 miljoonaa elektronia sekunnissa.Tämän suuruiset virrat ovat samalla niin pieniä, että niiden havaitsemiseen ja mittaamiseen liittyy merkittäviä kokeellisia vaikeuksia.

Positiivisen ionin varaus on elektronin varauksen kokonaislukukerrannainen, mutta sillä on päinvastainen etumerkki. Yksittäin ionisoituneiden hiukkasten varaus osoittautuu yhtä suureksi kuin elektronin varaus.

Ytimen tiheys on paljon suurempi kuin elektronin tiheys, ja suurin osa atomin koko tilavuudesta on tyhjää.

Sähköilmiöiden käsite

Hankaamalla kahta eri kappaletta yhteen sekä induktiolla kappaleille voidaan antaa erityisiä ominaisuuksia — sähköisiä. Tällaisia ​​kappaleita kutsutaan sähköistetyiksi.

Sähköistettyjen kappaleiden vuorovaikutukseen liittyviä ilmiöitä kutsutaan sähköisiä ilmiöitä.

Sähköistettujen kappaleiden välinen vuorovaikutus määräytyy ns Sähkövoimat, jotka eroavat muun luonteisista voimista siinä, että ne saavat varautuneet kappaleet hylkimään ja vetämään toisiaan niiden liikkeen nopeudesta riippumatta.

Tällä tavalla varattujen kappaleiden välinen vuorovaikutus eroaa esimerkiksi gravitaatiosta, jolle on ominaista vain kappaleiden vetovoima, tai magneettisesta alkuperästä peräisin olevista voimista, jotka riippuvat varausten suhteellisesta liikenteestä aiheuttaen magneettisia. ilmiöitä.

Sähkötekniikka tutkii pääasiassa ominaisuuksien ulkoisen ilmentymisen lakeja sähköistetyt elimet — sähkömagneettisten kenttien lait.

Jännite

Vastakkaisten varausten välisen voimakkaan vetovoiman vuoksi useimmat materiaalit ovat sähköisesti neutraaleja. Positiivisten ja negatiivisten varausten erottamiseen kuluu energiaa.

Kuvassa Kuvio 1 esittää kahta johtavaa, alun perin varaamatonta levyä, jotka on sijoitettu erilleen etäisyydellä d.Oletetaan, että levyjen välinen tila on täytetty eristeellä, kuten ilmalla, tai ne ovat tyhjiössä.

Riisi. 1. Kaksi johtavaa, alun perin varaamatonta levyä: a — Levyt ovat sähköisesti neutraaleja; b — varaus -Q siirtyy pohjalevylle (levyjen välillä on potentiaaliero ja sähkökenttä).

Kuvassa 1, molemmat levyt ovat neutraaleja, ja ylemmän levyn kokonaisnollavaraus voidaan esittää varausten +Q ja -Q summalla. Kuvassa Kuviossa 1b varaus -Q siirtyy ylemmältä levyltä alalevylle. Jos kuvassa 1b, yhdistämme levyt langalla, jolloin vastakkaisten varausten vetovoimat saavat varauksen siirtymään nopeasti takaisin ja palaamme kuvan 1 mukaiseen tilanteeseen. 1, a. Positiiviset varaukset siirtyisivät negatiivisesti varautuneelle levylle ja negatiiviset varaukset positiivisesti varautuneelle levylle.

Sanomme, että kuvassa esitettyjen varattujen levyjen välissä. Kuviossa 1b on potentiaaliero ja että positiivisesti varautuneella ylälevyllä potentiaali on suurempi kuin negatiivisesti varautuneella alalevyllä. Yleensä kahden pisteen välillä on potentiaaliero, jos näiden pisteiden välinen johtuminen johtaa varauksen siirtoon.

Positiiviset varaukset siirtyvät korkeapotentiaalisesta pisteestä matalapotentiaaliseen pisteeseen, negatiivisten varausten liikesuunta on päinvastainen - matalapotentiaalisesta pisteestä korkean potentiaalin pisteeseen.

Potentiaalieron mittayksikkö on voltti (V). Potentiaalieroa kutsutaan jännitteeksi ja se merkitään yleensä kirjaimella U.

Kahden pisteen välisen jännitteen kvantifioimiseksi käytetään käsitettä sähkökenttä… Kuvassa esitetyssä tapauksessaKuviossa 1b levyjen välillä on tasainen sähkökenttä, joka on suunnattu korkeamman potentiaalin alueelta (positiiviselta levyltä) alemman potentiaalin alueelle (negatiiviseen levyyn).

Tämän kentän voimakkuus, ilmaistuna voltteina metriä kohti, on verrannollinen levyjen varaukseen ja voidaan laskea fysiikan laeista, jos varausten jakautuminen tunnetaan. Sähkökentän suuruuden ja levyjen välisen jännitteen U välinen suhde on muotoa U = E NS e (voltti = voltti / metri x metri).

Siirtyminen alemmasta potentiaalista korkeampaan vastaa siis liikettä kentän suuntaa vastaan. Monimutkaisemmassa rakenteessa sähkökenttä ei välttämättä ole tasainen kaikkialla, ja kahden pisteen välisen potentiaalieron määrittämiseksi on tarpeen käyttää toistuvasti yhtälöä U = E NS e.

Meille kiinnostavien pisteiden välinen väli on jaettu useisiin osiin, joista jokainen on tarpeeksi pieni, jotta kenttä on siinä yhtenäinen. Yhtälöä sovelletaan sitten peräkkäin jokaiseen segmenttiin U = E NS e ja kunkin osan potentiaalierot lasketaan yhteen. Siten mistä tahansa varausten ja sähkökenttien jakautumisesta voit löytää minkä tahansa kahden pisteen välisen potentiaalieron.

Potentiaalieroa määritettäessä on tarpeen ilmoittaa paitsi jännitteen suuruus kahden pisteen välillä, myös se, millä pisteellä on suurin potentiaali. Useita eri elementtejä sisältävissä sähköpiireissä ei kuitenkaan aina ole mahdollista etukäteen määrittää, missä pisteessä on suurin potentiaali. Sekaannusten välttämiseksi on hyväksyttävä kylttien ehto (kuva 2).

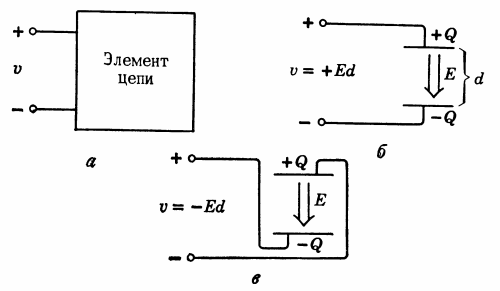
Riisi. 2… Jännitteen napaisuuden määrittäminen (jännite voi olla positiivinen tai negatiivinen).

Kaksinapaista piirielementtiä edustaa laatikko, joka on varustettu kahdella liittimellä (kuva 2, a). Kotelosta liittimiin johtavien johtojen oletetaan olevan ihanteellisia sähkövirran johtimia. Yksi terminaali on merkitty plusmerkillä ja toinen miinusmerkillä. Nämä merkit korjaavat suhteellisen napaisuuden. Jännite U kuvassa. 2, ja se määräytyy ehdolla U = (liittimen «+» potentiaali) — (liittimen «-« potentiaali).

Kuvassa Kuvassa 2b ladatut levyt on kytketty liittimiin siten, että «+»-napa on kytketty levyyn, jolla on korkeampi potentiaali. Tässä jännite U on positiivinen luku. Kuvassa 2, «+»-liitin on kytketty alempaan potentiaalilevyyn. Tuloksena saamme negatiivisen jännitteen.

On tärkeää muistaa stressin esityksen algebrallinen muoto. Kun napaisuus on määritetty, positiivinen jännite tarkoittaa, että «+»-liittimessä on (suurempi potentiaali) ja negatiivinen jännite tarkoittaa, että «-»-liittimessä on suurempi potentiaali.

Nykyinen

Edellä todettiin, että positiiviset varauksenkantajat siirtyvät suuren potentiaalin alueelta matalan potentiaalin alueelle, kun taas negatiiviset varauksenkantajat siirtyvät matalapotentiaaliselta alueelta korkean potentiaalin alueelle. Maksujen siirto tarkoittaa vanhenemista sähköä.

Kuvassa Kuva 3 esittää muutamia yksinkertaisia ​​tapauksia sähkövirran kulkemisesta, pintaksi valitaan C ja kuvitteellinen positiivinen suunta esitetään. Jos ajan dt osan S läpi kokonaisvaraus Q kulkee valittuun suuntaan, virta I - S on yhtä suuri kuin I = dV/dT. Virran mittayksikkö on ampeeri (A) (1A = 1C / s).

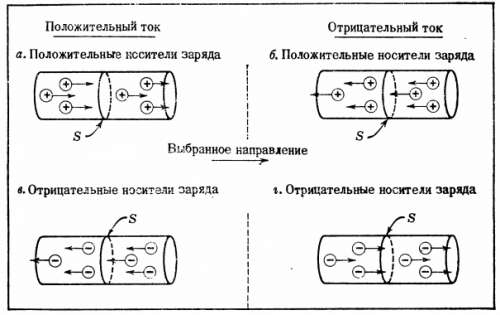
Riisi. 3… Virran suunnan ja matkaviestinvarausten virtaussuunnan välinen suhde.Virta on positiivinen (a ja b), jos tuloksena oleva positiivisten varausten virtaus jonkin pinnan C läpi osuu yhteen valitun suunnan kanssa. Virta on negatiivinen (b ja d), jos tuloksena oleva positiivisten varausten virtaus pinnan poikki on päinvastainen kuin valittu suunta.

Vaikeuksia syntyy usein nykyisen Iz-merkin määrittämisessä. Jos liikkuvat varauksenkantajat ovat positiivisia, positiivinen virta kuvaa liikkuvien kantajien todellista liikettä valittuun suuntaan, kun taas negatiivinen virta kuvaa liikkuvien varauksenkantajien virtausta, joka on vastakkainen valittuun suuntaan.

Jos matkapuhelinoperaattorit ovat negatiivisia, sinun on oltava varovainen virran suunnan määrittämisessä. Harkitse kuvaa. 3d, jossa negatiiviset liikkuvat varauksenkantajat ylittävät S:n valitussa suunnassa. Oletetaan, että jokaisella kantoaallolla on varaus -q ja virtausnopeus S:n läpi on n kantoaaltoa sekunnissa. Aikana dt on varausten C kokonaiskulku valittuun suuntaan dV = -n NS q NS dt, mikä vastaa virtaa I = dV/dT.

Siksi virta kuviossa 3d on negatiivinen. Lisäksi tämä virta osuu yhteen sen virran kanssa, joka syntyy positiivisten kantoaaltojen liikkeestä varauksella + q pinnan S läpi nopeudella n kantoaaltoa sekunnissa valittua vastakkaiseen suuntaan (kuva 3, b). Siten kaksinumeroiset varaukset heijastuvat kaksinumeroiseen virraan. Useimmissa tapauksissa elektroniikkapiireissä virran etumerkki on merkittävä, eikä sillä ole väliä mitkä varauksenkantajat (positiiviset tai negatiiviset) kuljettavat tätä virtaa. Siksi usein kun he puhuvat sähkövirrasta, he olettavat, että varauksen kantajat ovat positiivisia (katso - Sähkövirran suunta).

Puolijohdelaitteessa positiivisten ja negatiivisten varauksenkuljettajien välinen ero on kuitenkin kriittinen laitteen toiminnan kannalta.Näiden laitteiden toiminnan yksityiskohtaisen tarkastelun tulisi erottaa selvästi liikkuvien varauskantajien merkit. Tietyn alueen läpi kulkevan virran käsite voidaan helposti yleistää piirielementin läpi kulkevaksi virraksi.

Kuvassa Kuvio 4 esittää bipolaarista elementtiä. Positiivisen virran suunta näkyy nuolella.

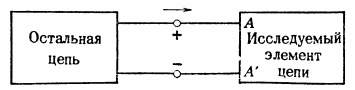
Riisi. 4. Virta piirielementin läpi. Varaukset saapuvat soluun terminaalin A kautta nopeudella i (coulombia sekunnissa) ja lähtevät solusta terminaalin A' kautta samalla nopeudella.

Jos positiivinen virta kulkee piirielementin läpi, positiivinen varaus tulee liittimeen A nopeudella i coulombia sekunnissa. Mutta kuten jo todettiin, materiaalit (ja piirielementit) pysyvät yleensä sähköisesti neutraaleina. (Jopa kuvion 1 "varatussa" kennossa kokonaisvaraus on nolla.) Siksi, jos varaus virtaa kennoon liittimen A kautta, saman määrän varausta täytyy samanaikaisesti virrata ulos kennosta navan A' kautta. Tämä piirielementin läpi kulkevan sähkövirran jatkuvuus seuraa elementin neutraalisuudesta kokonaisuutena.

Tehoa

Minkä tahansa piirin kaksinapaisen elementin napojen välillä voi olla jännite ja virta voi kulkea sen läpi. Virran ja jännitteen merkit voidaan määrittää itsenäisesti, mutta jännitteen ja virran napaisuuden välillä on tärkeä fyysinen suhde, jonka selventämiseksi yleensä otetaan joitain lisäehtoja.

Kuvassa Kuva 4 esittää, kuinka jännitteen ja virran suhteelliset polariteetit määritetään. Kun virran suunta on valittu, se virtaa «+»-liittimeen. Kun tämä lisäehto täyttyy, tärkeä sähkömäärä – sähköteho – voidaan määrittää. Harkitse piirielementtiä kuvassa. 4.

Jos jännite ja virta ovat positiivisia, positiivisten varausten virtaus on jatkuvaa korkeapotentiaalisesta pisteestä matalan potentiaalin pisteeseen. Tämän virtauksen ylläpitämiseksi on tarpeen erottaa positiiviset varaukset negatiivisista ja viedä ne «+»-liittimeen. Tämä jatkuva erottelu vaatii jatkuvaa energiankulutusta.

Kun varaukset kulkevat elementin läpi, ne vapauttavat tämän energian. Ja koska energiaa on varastoitava, se joko vapautuu piirielementissä lämpönä (esimerkiksi leivänpaahtimessa) tai varastoituu siihen (esimerkiksi auton akkua ladattaessa). Nopeutta, jolla tämä energian muunnos tapahtuu, kutsutaan tehoa ja se määritetään lausekkeella P = U NS Az (wattia = volttia x ampeeria).

Tehon mittayksikkö on watti (W), joka vastaa 1 J energian muuntamista 1 sekunnissa. Teho, joka on yhtä suuri kuin jännitteen ja virran tulo kuvassa 2 määritellyillä napaisuuksilla. 4 on algebrallinen suure.

Jos P > 0, kuten yllä olevassa tapauksessa, teho häviää tai absorboituu elementissä. Jos P < 0, niin tässä tapauksessa elementti syöttää virtaa piiriin, johon se on kytketty.

Resistiiviset elementit

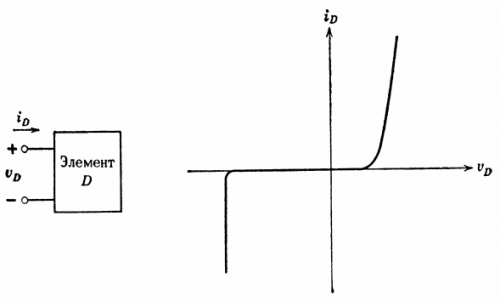
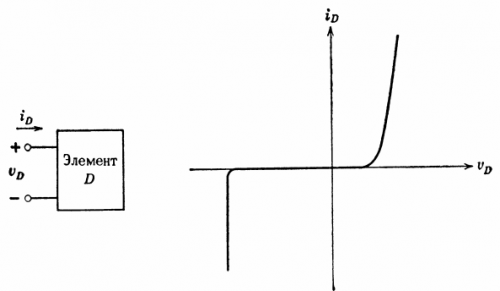
Jokaiselle piirielementille voit kirjoittaa tietyn suhteen päätejännitteen ja elementin läpi kulkevan virran välille. Resistiivinen elementti on elementti, jolle voidaan piirtää jännitteen ja virran välinen suhde.Tätä kuvaajaa kutsutaan virta-jännite ominaiskäyräksi. Esimerkki tällaisesta ominaisuudesta on esitetty kuvassa. 5.

Riisi. 5. Resistiivisen elementin virta-jännite-ominaisuus

Jos elementin D napojen jännite tunnetaan, kaavio voi määrittää virran elementin D läpi.Samoin, jos virta on tiedossa, jännite voidaan määrittää.

Täydellinen vastustuskyky

Ihanteellinen vastus (tai vastus) on lineaarinen resistiivinen elementti… Lineaarisuuden määritelmän mukaan jännitteen ja virran suhde lineaarisessa resistiivisessä elementissä on sellainen, että kun virta kaksinkertaistuu, myös jännite kaksinkertaistuu. Yleensä jännitteen tulee olla verrannollinen virtaan.

Suhteellista suhdetta jännitteen ja virran välillä kutsutaan Ohmin laki piirin osalle ja se kirjoitetaan kahdella tavalla: U = I NS R, jossa R on elementin vastus, ja I = G NS U, missä G = I / R on elementin johtavuus. Resistanssin yksikkö on ohmi (ohm) ja johtavuuden yksikkö on siemens (cm).

Ideaalivastuksen virta-jännite-ominaisuus on esitetty kuvassa. 6. Kaavio on origon läpi kulkeva suora viiva, jonka kaltevuus on yhtä suuri kuin Az/R.

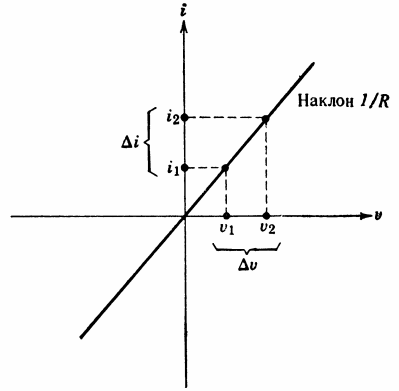
Riisi. 6. Ideaalivastuksen nimitys (a) ja virta-jännite-ominaisuus (b).

Tehoa täydellisellä vastuksella

Ideaalivastuksen absorboima teho:

P = UNS I = I2NS R, P = U2/R

Aivan kuten absorboitunut teho ideaalisessa resistanssissa riippuu virran (tai jännitteen) neliöstä, niin ideaalisessa resistanssissa absorboidun tehon v etumerkki riippuu R:n etumerkistä. Vaikka negatiivisia vastusarvoja käytetään joskus simuloitaessa tietyntyyppisiä laitteita, jotka toimivat tietyissä tiloissa, kaikki todelliset vastukset ovat yleensä positiivisia. Näillä vastuksilla absorboitunut teho on aina positiivinen.

Resistanssin absorboima sähköenergia, acc energian säilymisen laki, Täytyy NSmuuntua muihin lajeihin.Useimmiten sähköenergia muunnetaan lämpöenergiaksi, jota kutsutaan Joule-lämmöksi. Erittymisnopeus joulen lämpöä resistanssin suhteen se vastaa sähköenergian absorptionopeutta. Poikkeuksena ovat resistiiviset elementit (esim. hehkulamppu tai kaiutin), joissa osa absorboidusta energiasta muunnetaan muihin muotoihin (valo- ja äänienergia).

Tärkeimpien sähkösuureiden keskinäinen suhde

Tasavirtaa varten perusyksiköt on esitetty kuvassa. 7.

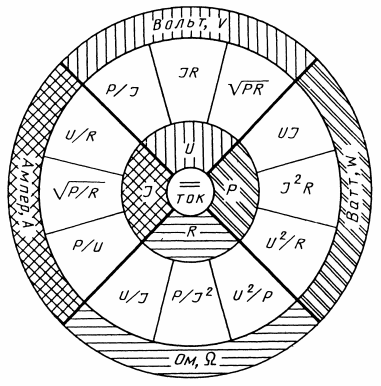
Riisi. 7. Tärkeimpien sähkösuureiden keskinäinen suhde

Neljä perusyksikköä - virta, jännite, resistanssi ja teho - on yhdistetty toisiinsa luotettavasti muodostetuilla suhteilla, joiden avulla voimme tehdä suorien, mutta myös epäsuoria mittauksia tai laskea tarvitsemamme arvot muista mitatuista. Joten jännitteen mittaamiseksi osassa piiriä on oltava volttimittari, mutta jopa sen puuttuessa voit laskea jännitteen arvon, kun tiedät piirin virran ja virran vastuksen tässä osiossa.