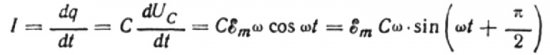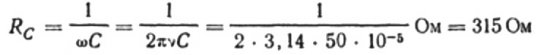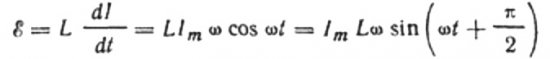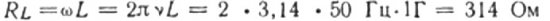Kapasitiivinen ja induktiivinen vastus vaihtovirtapiirissä

Jos sisällytämme kondensaattorin tasavirtapiiriin, huomaamme, että sillä on ääretön resistanssi, koska tasavirta ei yksinkertaisesti voi kulkea levyjen välisen eristeen läpi, koska eriste ei määritelmän mukaan johda tasavirtaa.

Kondensaattori katkaisee tasavirtapiirin. Mutta jos sama kondensaattori on nyt mukana vaihtovirtapiirissä, niin käy ilmi, että sen kondensaattori ei näytä rikkoutuvan kokonaan, se vain vuorottelee ja latautuu, eli sähkövaraus liikkuu ja virta ulkoisessa piirissä on ylläpidetään.

Maxwellin teorian perusteella voidaan tässä tapauksessa sanoa, että kondensaattorin sisällä oleva vaihtovirta on edelleen suljettu, vain tässä tapauksessa - bias-virralla. Tämä tarkoittaa, että AC-piirissä oleva kondensaattori toimii eräänlaisena rajallisen arvon vastuksena. Tätä vastusta kutsutaan kapasitiivinen.

Käytäntö on pitkään osoittanut, että johtimen läpi virtaavan vaihtovirran määrä riippuu johtimen muodosta ja sitä ympäröivän väliaineen magneettisista ominaisuuksista.Suoralla johdolla virta on suurin, ja jos sama lanka kääritään kelaan, jossa on suuri määrä kierroksia, virta on pienempi.

Ja jos ferromagneettinen ydin viedään samaan käämiin, virta pienenee entisestään. Siksi lanka tuottaa vaihtovirtaa ohmisen (aktiivisen) resistanssin ohella myös lisävastuksen, riippuen langan induktanssista. Tätä vastusta kutsutaan ns. induktiivinen.

Sen fyysinen merkitys on, että muuttuva virta tietyn induktanssin omaavassa johtimessa käynnistää itseinduktion EMF:n kyseisessä johtimessa, mikä pyrkii estämään virran muutoksia, eli pyrkii vähentämään virtaa. Tämä vastaa langan vastuksen lisäämistä.

AC-piirin kapasitanssi

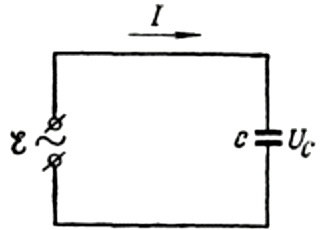
Puhutaanpa ensin kapasitiivisesta resistanssista yksityiskohtaisemmin. Oletetaan, että kondensaattori, jonka kapasitanssi on C, on kytketty sinimuotoiseen vaihtovirtalähteeseen, niin tämän lähteen EMF kuvataan seuraavalla kaavalla:

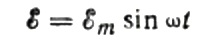
Jätämme huomioimatta jännitehäviön liitäntäjohtojen välillä, koska se on yleensä hyvin pieni ja voidaan tarvittaessa harkita erikseen. Oletetaan nyt, että kondensaattorilevyjen jännite on yhtä suuri kuin vaihtovirtalähdejännite. Sitten:

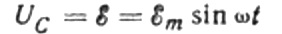
Kulloinkin kondensaattorin varaus riippuu sen kapasitanssista ja sen levyjen välisestä jännitteestä. Sitten, kun otetaan huomioon edellä mainittu lähde, saadaan lauseke kondensaattorilevyjen varauksen löytämiseksi lähdejännitteen perusteella:

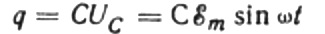
Olkoon äärettömän pienen ajan dt kondensaattorin varaus muuttuu dq, jolloin virta I kulkee johtojen läpi lähteestä kondensaattoriin, joka on yhtä suuri:

Nykyisen amplitudin arvo on yhtä suuri:

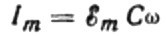
Sitten virran viimeinen lauseke on:

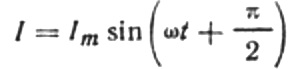
Kirjoitetaan nykyinen amplitudikaava uudelleen seuraavasti:

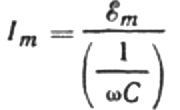
Tämä suhde on Ohmin laki, jossa kulmataajuuden ja kapasitanssin tulon käänteisluku toimii vastuksena, ja se on itse asiassa lauseke kondensaattorin kapasitanssin löytämiseksi sinimuotoisessa vaihtovirtapiirissä:

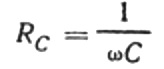
Tämä tarkoittaa, että kapasitiivinen vastus on kääntäen verrannollinen virran kulmataajuuteen ja kondensaattorin kapasitanssiin. Tämän riippuvuuden fyysinen merkitys on helppo ymmärtää.

Mitä suurempi vaihtovirtapiirin kondensaattorin kapasitanssi ja mitä useammin virran suunta kyseisessä piirissä muuttuu, sitä enemmän kokonaisvarausta kulkee aikayksikköä kohti kondensaattorin vaihtovirtalähteeseen yhdistävien johtimien poikkileikkauksen läpi. Tämä tarkoittaa, että virta on verrannollinen kapasitanssin ja kulmataajuuden tuloon.

Lasketaan esimerkiksi kondensaattorin, jonka sähköinen kapasiteetti on 10 mikrofaradia, kapasitanssi sinimuotoiselle vaihtovirtapiirille, jonka taajuus on 50 Hz:

Jos taajuus olisi 5000 Hz, saman kondensaattorin vastus olisi noin 3 ohmia.

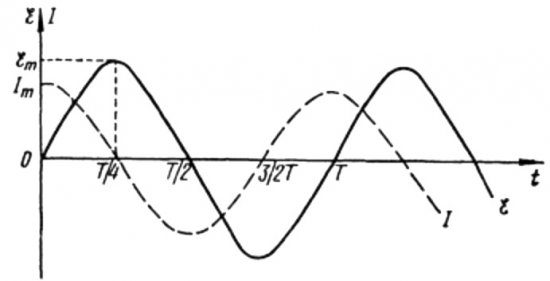
Yllä olevista kaavoista on selvää, että virta ja jännite AC-piirissä, jossa on kondensaattori, muuttuvat aina eri vaiheissa. Virtavaihe johtaa jännitevaiheeseen pi / 2:lla (90 astetta). Tämä tarkoittaa, että maksimivirta ajassa on aina olemassa neljännesjaksoa aikaisemmin kuin maksimijännite. Näin ollen kapasitiivisen vastuksen poikki virta johtaa jännitettä neljänneksellä ajanjaksosta tai 90 astetta vaiheittain.

Selitätään tämän ilmiön fyysinen merkitys.Ensimmäisellä ajanhetkellä kondensaattori purkautuu täysin, joten pieninkin siihen kohdistettu jännite siirtää jo kondensaattorin levyjen varauksia muodostaen virran.

Kondensaattorin latautuessa sen levyjen jännite kasvaa, mikä estää latauksen jatkamisen, joten virtapiirissä vähenee huolimatta levyihin kohdistetun jännitteen lisääntymisestä.

Tämä tarkoittaa, että jos alkuhetkellä virta oli maksimi, niin kun jännite saavuttaa maksiminsa neljännesjakson jälkeen, virta pysähtyy kokonaan.

Jakson alussa virta on maksimi ja jännite minimi ja alkaa nousta, mutta neljänneksen jakson jälkeen jännite saavuttaa maksimin, mutta virta on tähän mennessä pudonnut jo nollaan. Siten käy ilmi, että jännite johtaa jännitettä neljänneksellä jaksosta.

AC induktiivinen vastus

Nyt takaisin induktiiviseen vastukseen. Oletetaan, että sinimuotoinen vaihtovirta kulkee induktanssikelan läpi. Se voidaan ilmaista seuraavasti:

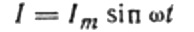
Virta johtuu käämiin syötetystä vaihtojännitteestä. Tämä tarkoittaa, että kelaan ilmestyy itseinduktion EMF, joka ilmaistaan ​​seuraavasti:

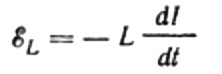
Jälleen jätämme huomiotta jännitteen pudotuksen johtimissa, jotka yhdistävät EMF-lähteen kelaan. Niiden ohminen vastus on erittäin alhainen.

Olkoon kelaan kulloinkin kohdistettu vaihtojännite täysin tasapainotettu itseinduktion EMF:llä, joka on sen suuruinen, mutta suunnaltaan vastakkainen:

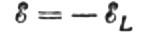
Sitten meillä on oikeus kirjoittaa:

Koska kelaan syötetyn jännitteen amplitudi on:

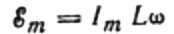
saamme:

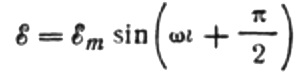
Ilmaistaan ​​maksimivirta seuraavasti:

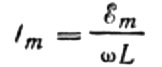
Tämä lauseke on pohjimmiltaan Ohmin laki. Suurella, joka on yhtä suuri kuin induktanssin ja kulmataajuuden tulo, on tässä vastuksen rooli, eikä se ole muuta kuin induktorin induktiivinen vastus:

Joten induktiivinen vastus on verrannollinen kelan induktanssiin ja käämin läpi kulkevan vaihtovirran kulmataajuuteen.

Tämä johtuu siitä, että induktiivinen resistanssi johtuu itseinduktion EMF:n vaikutuksesta lähdejännitteeseen, - itseinduktio-EMF pyrkii vähentämään virtaa ja tuo siten vastusta piiriin. Itseinduktion emf:n suuruus, kuten tiedetään, on verrannollinen käämin induktanssiin ja sen läpi kulkevan virran muutosnopeuteen.

Lasketaan esimerkiksi induktiivinen resistanssi kelalle, jonka induktanssi on 1 H ja joka sisältyy piiriin, jonka virtataajuus on 50 Hz:

Jos pallon taajuus olisi 5000 Hz, niin saman kelan resistanssi olisi noin 31 400 ohmia. Muista, että kelalangan ohminen vastus on yleensä muutama ohmi.

Yllä olevista kaavoista on selvää, että käämin läpi kulkevan virran ja siinä olevan jännitteen muutokset tapahtuvat eri vaiheissa ja virran vaihe on aina pienempi kuin jännitteen vaihe pi / 2:ssa. maksimivirta tapahtuu neljännesjaksoa myöhemmin kuin maksimirasituksen alkaminen.

Induktiivisessa resistanssissa virta on 90 astetta jäljessä jännitteestä johtuen itseindusoidun EMF:n jarrutusvaikutuksesta, mikä estää virran muuttumisen (sekä kasvamisen että pienenemisen), joten maksimivirta havaitaan käämin varustetussa piirissä myöhemmin. kuin maksimijännite.

Kelan ja kondensaattorin yhdistetty toiminta

Jos kytket käämin kondensaattorilla sarjaan vaihtovirtapiirin kanssa, kelan jännite lisää kondensaattorin jännitettä ajassa puoli jaksoa eli 180 astetta vaiheittain.

Kapasitiivista ja induktiivista vastusta kutsutaan reagoivat aineet… Energiaa ei kuluteta reaktiiviseen vastukseen vaan aktiiviseen vastukseen. Kondensaattoriin varastoitu energia palautetaan ajoittain takaisin lähteeseen, kun kondensaattorin sähkökenttä katoaa.

Sama on kelan kanssa: koska käämin magneettikenttä syntyy virran vaikutuksesta, siinä oleva energia kerääntyy jakson neljänneksen aikana ja seuraavan neljänneksen aikana se palaa lähteeseen. Tässä artikkelissa olemme puhuneet sinimuotoisesta vaihtovirrasta, jonka osalta näitä määräyksiä noudatetaan tiukasti.

AC sinimuotoisissa piireissä kutsutaan sydänkeloja tukahduttavakäytetään perinteisesti virranrajoitukseen. Niiden etuna reostaatteihin verrattuna on, että energiaa ei haihdu valtavia määriä lämpönä.