Aktiivinen ja reaktiivinen vastus, vastuskolmio

Aktiivisuus ja reaktiivisuus

Tasavirtapiireissä olevien passien ja kuluttajien tuottamaa vastusta kutsutaan ohmiresistanssiksi.

Jos jokin johto sisältyy vaihtovirtapiiriin, käy ilmi, että sen vastus on hieman suurempi kuin tasavirtapiirissä. Tämä johtuu ilmiöstä, jota kutsutaan ihovaikutukseksi (pintavaikutus).

Sen olemus on seuraava. Kun vaihtovirta kulkee johdon läpi, sen sisällä on vaihtomagneettikenttä, joka ylittää johdon. Tämän kentän magneettiset voimalinjat indusoivat EMF:n johtimessa, mutta se ei ole sama johtimen poikkileikkauksen eri kohdissa: enemmän poikkileikkauksen keskustaa kohti ja vähemmän kehää kohti.

Tämä johtuu siitä, että lähempänä keskustaa olevia pisteitä ylittää suuri määrä voimalinjoja. Tämän EMF:n vaikutuksesta vaihtovirtaa ei jaeta tasaisesti koko johtimen osalle, vaan lähemmäs sen pintaa.

Tämä vastaa johtimen hyödyllisen poikkileikkauksen pienentämistä ja siten sen vaihtovirran vastuksen lisäämistä. Esimerkiksi kuparilanka, jonka pituus on 1 km ja halkaisija 4 mm, kestää: DC - 1,86 ohmia, AC 800 Hz - 1,87 ohmia, AC 10 000 Hz - 2,90 ohmia.

Johtimen tarjoamaa resistanssia sen läpi kulkevalle vaihtovirralle kutsutaan aktiiviseksi resistanssiksi.

Jos jokin kuluttaja ei sisällä induktanssia ja kapasitanssia (hehkulamppu, lämmityslaite), se on myös aktiivinen vaihtovirtavastus.

Aktiivinen vastus - fysikaalinen suure, joka kuvaa sähköpiirin (tai sen alueen) resistanssia sähkövirralle, joka johtuu sähköenergian palautumattomista muutoksista muihin muotoihin (pääasiassa lämmöksi). Ohmeina ilmaistuna.

Aktiivinen vastus riippuu AC-taajuuskasvaa sen lisääntyessä.

Monilla kuluttajilla on kuitenkin induktiivisia ja kapasitiivisia ominaisuuksia, kun vaihtovirta kulkee niiden läpi. Näitä kuluttajia ovat muuntajat, kuristimet, sähkömagneetit, kondensaattorit, erilaisia ​​johtoja ja monia muita.

Niiden läpi kulkiessaan vaihtovirta On tarpeen ottaa huomioon paitsi aktiivinen myös reaktiivisuus, koska kuluttajassa on induktiivisia ja kapasitiivisia ominaisuuksia.

Tiedetään, että jos jokaisen kelan läpi kulkeva tasavirta katkaistaan ​​ja suljetaan, niin samalla kun virta muuttuu, myös kelan sisällä oleva magneettivuo muuttuu, minkä seurauksena tapahtuu itseinduktion EMF sen sisällä.

Sama havaitaan AC-piiriin kuuluvassa kelassa, sillä ainoalla erolla, että tock muuttuu jatkuvasti sekä suuruuden että sisään ja suuntaan. Siksi kelaan tunkeutuvan magneettivuon suuruus muuttuu jatkuvasti ja indusoi Itseinduktion EMF.

Mutta itseinduktion emf:n suunta on aina sellainen, että se vastustaa virran muutosta. Joten kun kelan virta kasvaa, itse aiheutettu EMF pyrkii hidastamaan virran kasvua, ja kun virta pienenee, se pyrkii päinvastoin ylläpitämään katoavaa virtaa.

Tästä seuraa, että vaihtovirtapiiriin kuuluvassa kelassa (johtimessa) esiintyvä itseinduktion EMF toimii aina virtaa vastaan ​​hidastaen sen muutoksia. Toisin sanoen itseinduktion EMF:ää voidaan pitää lisäresistanssina, joka yhdessä kelan aktiivisen vastuksen kanssa vastustaa kelan läpi kulkevaa vaihtovirtaa.

Resistanssia, jonka emf tarjoaa vaihtovirralle itseinduktiolla, kutsutaan induktiiviseksi resistanssiksi.

Induktiivinen vastus on sitä suurempi, mitä suurempi on käyttäjän (piirin) induktanssi ja mitä suurempi vaihtovirran taajuus. Tämä vastus ilmaistaan ​​kaavalla xl = ωL, jossa xl on induktiivinen vastus ohmeina; L - induktanssi henryssä (gn); ω — kulmataajuus, missä f — virran taajuus).

Induktiivisen vastuksen lisäksi siinä on kapasitanssia, mikä johtuu sekä kapasitanssin läsnäolosta johtimissa ja keloissa että kondensaattoreiden sisällyttämisestä vaihtovirtapiiriin joissakin tapauksissa.Kuluttajan (piirin) kapasitanssin C ja virran kulmataajuuden kasvaessa kapasitiivinen vastus pienenee.

Kapasitiivinen vastus on yhtä suuri kuin xc = 1 / ωC, missä xc - kapasitiivinen vastus ohmeina, ω - kulmataajuus, C - kuluttajakapasiteetti faradeina.

Lue aiheesta lisää täältä: Reaktanssi sähkötekniikassa

Resistanssikolmio

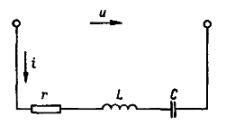
Tarkastellaan piiriä, jonka aktiivisen elementin resistanssi r, induktanssi L ja kapasitanssi C.

Riisi. 1. AC-piiri vastuksella, kelalla ja kondensaattorilla.

Tällaisen piirin impedanssi on z = √r2+ (хl — xc)2) = √r2 + х2)

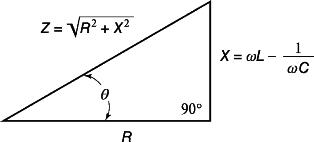
Graafisesti tämä lauseke voidaan kuvata ns. vastuskolmion muodossa.

Kuva. 2. Resistanssikolmio

Vastuskolmion hypotenuusa edustaa piirin kokonaisvastusta, jalat - aktiivista ja reaktiivista vastusta.

Jos yksi piirin vastuksista on (aktiivinen tai reaktiivinen), esimerkiksi 10 kertaa pienempi tai enemmän kuin toinen, niin pienempi voidaan jättää huomiotta, mikä on helposti tarkistettavissa suoralla laskennalla.