Anturin ominaisuuksien linearisointi

Anturin ominaisuuksien linearisointi — anturin lähtöarvon tai siihen verrannollisen suuren (analoginen tai digitaalinen) epälineaarinen muunnos, jolla saavutetaan lineaarinen suhde mitatun arvon ja sitä edustavan arvon välillä.

Linearisoinnin avulla on mahdollista saavuttaa lineaarisuus sen toissijaisen laitteen asteikolla, johon on kytketty epälineaarisella ominaisuudella varustettu anturi (esim. termopari, lämpövastus, kaasuanalysaattori, virtausmittari jne.). Anturin ominaisuuksien linearisointi mahdollistaa tarvittavan mittaustarkkuuden saavuttamisen digitaalisella lähdöllä varustettujen toissijaisten laitteiden kautta. Tämä on tarpeen joissain tapauksissa, kun antureita liitetään tallennuslaitteisiin tai kun suoritetaan matemaattisia operaatioita mitatulle arvolle (esim. integrointi).

Enkooderin ominaisuuden kannalta linearisointi toimii käänteisenä toiminnallisena muunnoksena.Jos anturin ominaiskäyrä esitetään muodossa y = F (a + bx), missä x on mitattu arvo, a ja b ovat vakioita, anturin kanssa sarjaan kytketyn linearisaattorin ominaiskäyrän (kuva 1) pitäisi näyttää. näin: z = kF (y), missä F on F:n käänteisfunktio.

Tämän seurauksena linearisoijan ulostulo on z = kF(F (a + bx)) = a ' + b'x, eli mitatun arvon lineaarinen funktio.

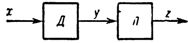
Riisi. 1. Yleistetty linearisoinnin lohkokaavio: D — anturi, L — linearisoija.

Lisäksi skaalauttamalla riippuvuus z pienennetään muotoon z'= mx, missä m on sopiva skaalaustekijä. Jos linearisointi tehdään kompensoivalla tavalla eli perustuen kuvan 1 kaltaiseen servojärjestelmään. 2, niin linearisoivan funktiomuuntimen ominaisuuden tulee olla samanlainen kuin anturin ominaisuus z = cF (a + bx), koska mitatun arvon linearisoitu arvo on otettu funktiolinearisaattorin muuntimen tulosta ja sen lähtöä verrataan anturin lähtöarvoon.

Linearisoijille toiminnallisina muuntimina tyypillinen piirre on niiden toistama suhteellisen kapea riippuvuusluokka, joka rajoittuu monotonisiin toimintoihin ja joka määräytyy anturin ominaisuuksien tyypin mukaan.

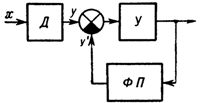
Riisi. 2. Linearisoinnin lohkokaavio seurantajärjestelmään perustuen: D — anturi, U — vahvistin (muunnin), FP — toiminnallinen muunnin.

Linearisaattorit voidaan luokitella seuraavien kriteerien mukaan:

1. Toiminnon asetusmenetelmän mukaan: spatiaalinen mallien, matriisien jne. muodossa, epälineaaristen elementtien yhdistelmän muodossa, digitaalisen laskenta-algoritmin muodossa, laitteet.

2.Järjestelmän joustavuusasteen mukaan: universaali (eli uudelleenkonfiguroitava) ja erikoistunut.

3. Rakennekaavion luonteen mukaan: avoin (kuva 1) ja kompensointityyppi (kuva 2).

4. Tulo- ja lähtöarvojen muodossa: analoginen, digitaalinen, sekoitettu (analoginen-digitaalinen ja digitaalinen-analoginen).

5. Piirissä käytettyjen elementtien tyypin mukaan: mekaaninen, sähkömekaaninen, magneettinen, elektroninen jne.

Tilafunktion linearisoijat sisältävät pääasiassa nokkamekanismeja, kuvioita ja epälineaarisia potentiometrejä. Niitä käytetään tapauksissa, joissa kunkin muunnosvaiheen mitattu arvo esitetään mekaanisen liikkeen muodossa (nokat — manometristen ja muuntaja-anturien ominaisuuksien linearisointiin, mallit — tallentimissa, epälineaarisissa potentiometreissä — potentiaali- ja siltapiireissä ).

Potentiometrin ominaisuuksien epälineaarisuus saavutetaan kelaamalla profiloituihin kehyksiin ja leikkaamalla paloittain lineaarista approksimaatiomenetelmää ohjaamalla osia sopivilla vastuksilla.

Linearisaattorissa, joka perustuu sähkömekaaniseen servojärjestelmään, joka on potentiometrinen tyyppi ja jossa käytetään epälineaarista potentiometriä (kuva 3), linearisoitu arvo näkyy kiertokulmana tai mekaanisena siirtymänä. Nämä linearisoijat ovat yksinkertaisia, monipuolisia ja niitä käytetään laajasti keskitetyissä ohjausjärjestelmissä.

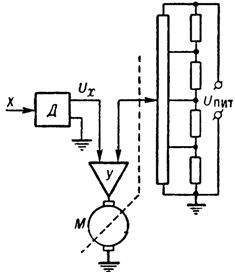
Riisi. 3. Potentiometrisen tyyppisen sähkömekaanisen servojärjestelmän linearisaattori: D — anturi, jonka lähtö on tasajännitteen muodossa, Y — vahvistin, M — sähkömoottori.

Parametrisissa toiminnallisissa muuntimissa käytetään yksittäisten elementtien ominaisuuksien epälineaarisuutta (elektroniset, magneettiset, termiset jne.). Niiden kehittämien toiminnallisten riippuvuuksien ja antureiden ominaisuuksien välillä ei kuitenkaan yleensä ole mahdollista saavuttaa täydellistä vastaavuutta.

Digitaalisissa funktiomuuntimissa käytetään algoritmista funktion asetustapaa. Niiden etuja ovat korkea tarkkuus ja ominaisuuksien vakaus. Niissä käytetään yksittäisten funktionaalisten riippuvuuksien matemaattisia ominaisuuksia tai osittaisen lineaarisen approksimoinnin periaatetta. Esimerkiksi paraabeli kehitetään kokonaislukujen neliöiden ominaisuuksien perusteella.

Esimerkiksi digitaalinen linearisoija perustuu paloittain lineaariseen approksimaatiomenetelmään, joka toimii periaatteella täyttää lähestyvät segmentit eri toistotaajuuksilla pulsseilla. Täyttötaajuudet muuttuvat hyppyissä lähestyvien segmenttien rajapisteissä laitteeseen lisätyn ohjelman mukaan epälineaarisuuden tyypin mukaan. Linearisoitu määrä muunnetaan sitten unitaarikoodiksi.

Epälineaarisuuden osittainen lineaarinen approksimaatio voidaan suorittaa myös käyttämällä digitaalista lineaarista interpolaattoria. Tällöin interpolointivälien täyttötaajuudet pysyvät vakiona vain keskimäärin.

Osien lineaarisen approksimaatiomenetelmään perustuvien digitaalisten linearisoijien etuja ovat: kertyneen epälineaarisuuden uudelleenkonfiguroinnin helppous ja epälineaarisuudesta toiseen siirtymisen nopeus, mikä on erityisen tärkeää nopeissa keskitetyissä ohjausjärjestelmissä.

Monimutkaisissa ohjausjärjestelmissä, jotka sisältävät universaaleja laskimia, koneita, linearisointi voidaan suorittaa suoraan näistä koneista, joissa toiminto on upotettu vastaavan aliohjelman muodossa.