AC kondensaattori

Kootaan piiri kanssa kondensaattori, jossa vaihtovirtageneraattori tuottaa sinimuotoisen jännitteen. Analysoidaan peräkkäin, mitä piirissä tapahtuu, kun suljemme kytkimen. Tarkastellaan alkuhetkeä, jolloin generaattorin jännite on nolla.

Jakson ensimmäisen neljänneksen aikana generaattorin liittimien jännite nousee nollasta alkaen ja kondensaattori alkaa latautua. Piiriin ilmestyy virta, mutta kondensaattorin ensimmäisellä lataushetkellä huolimatta siitä, että sen levyjen jännite on juuri ilmestynyt ja on edelleen hyvin pieni, virtapiirissä oleva virta (latausvirta) on suurin . Kun kondensaattorin varaus kasvaa, virta piirissä pienenee ja saavuttaa nollan sillä hetkellä, kun kondensaattori on latautunut täyteen. Tässä tapauksessa kondensaattorin levyjen jännite, joka seuraa tiukasti generaattorin jännitettä, tulee tällä hetkellä maksimiin, mutta päinvastaisella merkillä, eli se on suunnattu generaattorin jännitteeseen.

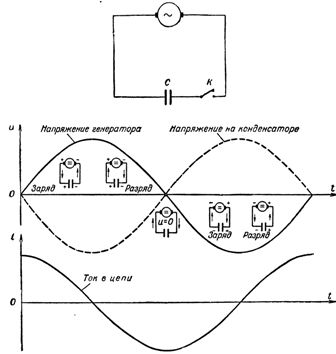
Riisi. 1. Virran ja jännitteen muutos kapasitanssilla varustetussa piirissä

Tällä tavalla virta syöksyy suurimmalla voimalla kondensaattoriin ilmaiseksi, mutta alkaa heti laskea, kun kondensaattorin levyt täyttyvät varauksista ja putoavat nollaan latautuen täyteen.

Verrataan tätä ilmiötä siihen, mitä tapahtuu veden virtaukselle putkessa, joka yhdistää kaksi toisiinsa yhteydessä olevaa astiaa (kuva 2), joista toinen on täynnä ja toinen tyhjä. Ei tarvitse kuin painaa vesireitin sulkevaa venttiiliä, sillä vesi syöksyy heti vasemmasta astiasta suurella paineella putken läpi tyhjään oikeaan astiaan. Välittömästi kuitenkin putken vedenpaine alkaa vähitellen heikentyä astioiden tasojen tasoittumisen vuoksi ja putoaa nollaan. Veden virtaus pysähtyy.

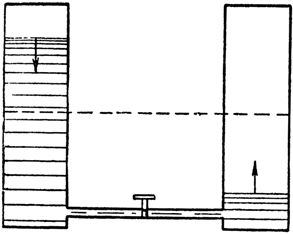
Riisi. 2. Vedenpaineen muutos viestintäastioita yhdistävässä putkessa on samanlainen kuin virtapiirin muutos kondensaattorin latauksen aikana

Samoin virta syöksyy ensin varaamattomaan kondensaattoriin ja sitten vähitellen heikkenee latautuessaan.

Jakson toisen neljänneksen alkaessa, kun generaattorin jännite alkaa aluksi hitaasti ja sitten laskee yhä nopeammin, varautunut kondensaattori purkautuu generaattoriin aiheuttaen purkausvirran piiriin. Generaattorin jännitteen pienentyessä kondensaattori purkautuu yhä enemmän ja purkausvirta piirissä kasvaa. Purkausvirran suunta tällä jakson neljänneksellä on päinvastainen kuin jakson ensimmäisen neljänneksen latausvirran suunta. Vastaavasti nykyinen käyrä, joka on ohittanut nollaarvon, sijaitsee nyt aika-akselin alapuolella.

Ensimmäisen puolijakson lopussa generaattorin jännite, samoin kuin kondensaattorin jännite, lähestyy nopeasti nollaa ja piirivirta saavuttaa hitaasti maksimiarvonsa. Koska virran arvo piirissä on suurempi, mitä suurempi on piirissä olevan varauksen arvo, tulee selväksi, miksi virta saavuttaa maksiminsa, kun kondensaattorin levyillä oleva jännite ja siten varaus kondensaattori, laskee nopeasti.

Jakson kolmannen neljänneksen alussa kondensaattori alkaa latautua uudelleen, mutta sen levyjen napaisuus sekä generaattorin napaisuus muuttuvat "ja päinvastoin, ja virta jatkaa virtaamista suunta, alkaa laskea kondensaattorin latautuessa.jakson kolmannen neljänneksen lopussa, kun generaattorin ja kondensaattorin jännitteet saavuttavat maksiminsa, virta menee nollaan.

Jakson viimeisen neljänneksen aikana jännite laskee nollaan ja virta, muutettuaan suuntaaan piirissä, saavuttaa maksimiarvonsa. Tässä jakso päättyy, jonka jälkeen seuraava alkaa, toistaen tarkalleen edellistä ja niin edelleen.

Näin ollen generaattorin vaihtojännitteen vaikutuksesta kondensaattori ladataan kahdesti ajanjakson aikana (jakson ensimmäinen ja kolmas neljännes) ja puretaan kahdesti (jakson toinen ja neljäs neljännes). Mutta koska ne vuorottelevat yksitellen kondensaattori latautuu ja purkautuu Kun lataus- ja purkausvirta kulkee joka kerta piirin läpi, voimme päätellä sen vaihtovirta.

Voit tarkistaa tämän seuraavassa yksinkertaisessa kokeessa. Liitä 4-6 mikrofaradin kondensaattori verkkovirtaan 25 W hehkulampun kautta.Valo syttyy eikä sammu ennen kuin virtapiiri katkeaa. Tämä viittaa siihen, että vaihtovirta on kulkenut kapasitanssin piirin läpi. Tietenkään se ei kulje kondensaattorin eristeen läpi, vaan edustaa milloin tahansa joko varausvirtaa tai kondensaattorin purkausvirtaa.

Kuten tiedämme, dielektrinen polarisoituu siihen syntyvän sähkökentän vaikutuksesta, kun kondensaattori latautuu, ja sen polarisaatio katoaa, kun kondensaattori puretaan.

Tässä tapauksessa eriste, jossa on syrjäytysvirta, toimii vaihtovirralle eräänlaisena piirin jatkona, ja vakiona se katkaisee piirin. Mutta siirtymävirta muodostuu vain kondensaattorin dielektrissä, ja siksi varausten siirtoa piiriä pitkin ei tapahdu.

Vaihtovirtakondensaattorin tarjoama resistanssi riippuu kondensaattorin kapasitanssin arvosta ja virran taajuudesta.

Mitä suurempi kondensaattorin kapasiteetti, sitä suurempi on virtapiirin varaus kondensaattorin latauksen ja purkamisen aikana ja vastaavasti sitä suurempi virtapiirissä. Virran kasvu piirissä osoittaa, että sen vastus on pienentynyt.

Siksi kapasitanssin kasvaessa piirin vaihtovirtavastus pienenee.

Se kasvaa nykyinen taajuus lisää piirissä kuljetetun varauksen määrää, koska kondensaattorin varaamisen (sekä purkautumisen) on tapahduttava nopeammin kuin matalalla taajuudella. Samanaikaisesti siirretyn varauksen määrän kasvu aikayksikköä kohti vastaa virran kasvua piirissä ja siten sen vastuksen pienenemistä.

Jos jollakin tavalla asteittain pienennämme vaihtovirran taajuutta ja vähennämme virran tasavirraksi, niin piiriin kuuluvan kondensaattorin resistanssi kasvaa vähitellen ja tulee äärettömän suureksi (katkaisee piirin), kunnes se ilmestyy vakiovirtapiiri.

Siksi taajuuden kasvaessa kondensaattorin vastus vaihtovirtaan pienenee.

Aivan kuten käämin vastusta vaihtovirralle kutsutaan induktiiviseksi, kondensaattorin vastusta kutsutaan kapasitiiviseksi.

Siksi kapasitiivinen vastus on suurempi, mitä pienempi piirin kapasiteetti ja sitä syöttävän virran taajuus.

Kapasitiivinen resistanssi on merkitty Xc:llä ja mitataan ohmeina.

Kapasitiivisen vastuksen riippuvuus virran taajuudesta ja piirin kapasiteetista määritetään kaavalla Xc = 1 /ωC, jossa ω on ympyrätaajuus, joka on yhtä suuri kuin 2πe:n tulo, C on piirin kapasiteetti faradit.

Kapasitiivisella resistanssilla, kuten induktiivisella resistanssilla, on reaktiivinen luonne, koska kondensaattori ei kuluta virtalähteen energiaa.

kaava Ohmin laki kapasitiiviselle piirille se on muotoa I = U / Xc, missä I ja U - virran ja jännitteen teholliset arvot; Xc on piirin kapasitiivinen resistanssi.

Kondensaattorien ominaisuutta tarjota suuri vastustuskyky matalataajuisille virroille ja siirtää helposti korkeataajuisia virtoja käytetään laajalti viestintälaitteiden piireissä.

Kondensaattorien avulla saavutetaan esimerkiksi vakiovirtojen ja pientaajuisten virtojen erottaminen suurtaajuisista virroista, jotka ovat välttämättömiä piirien toiminnalle.

Jos on tarpeen estää matalataajuisen virran reitti piirin korkeataajuisessa osassa, pieni kondensaattori kytketään sarjaan. Se tarjoaa erinomaisen vastustuskyvyn matalataajuuksiselle virralle ja kulkee samalla helposti korkeataajuisen virran läpi.

Jos on tarpeen estää suurtaajuusvirta esimerkiksi radioaseman virtapiirissä, käytetään suuren kapasiteetin kondensaattoria, joka on kytketty rinnan virtalähteen kanssa. Tässä tapauksessa suurtaajuusvirta kulkee kondensaattorin läpi ohittaen radioaseman virtapiirin.

Aktiivinen vastus ja kondensaattori vaihtovirtapiirissä

Käytännössä tapauksia havaitaan usein ollessaan sarjapiirissä kapasitanssilla aktiivinen vastus on mukana. Piirin kokonaisresistanssi tässä tapauksessa määräytyy kaavan mukaan

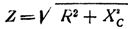
Siksi aktiivisesta ja kapasitiivisesta vaihtovirtaresistanssista koostuvan piirin kokonaisresistanssi on yhtä suuri kuin tämän piirin aktiivisen ja kapasitiivisen resistanssin neliösumman neliöjuuri.

Ohmin laki pätee myös tälle I = U / Z -piirille.

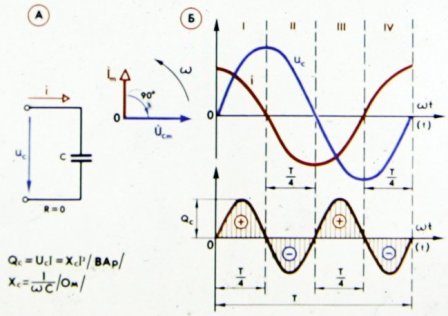
Kuvassa Kuva 3 esittää käyriä, jotka kuvaavat virran ja jännitteen välistä vaihesuhdetta kapasitiivisen ja aktiivisen resistanssin sisältävässä piirissä.

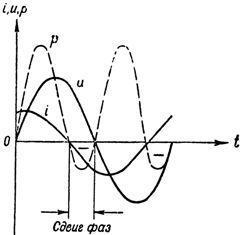
Riisi. 3. Virta, jännite ja teho piirissä, jossa on kondensaattori ja aktiivinen vastus

Kuten kuvasta voidaan nähdä, virta tässä tapauksessa lisää jännitettä ei neljänneksellä jaksolla, vaan vähemmän, koska aktiivinen vastus rikkoo piirin puhtaasti kapasitiivista (reaktiivista) luonnetta, kuten pienentynyt vaihe osoittaa. siirtää. Nyt piirin napojen jännite määritellään kahden komponentin summana: jännitteen reaktiivinen komponentti voittaa piirin kapasitiivisen vastuksen ja jännitteen aktiivisen komponentin, voittamalla sen aktiivisen vastuksen.

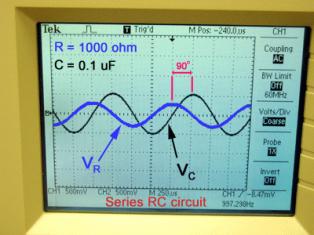
Mitä suurempi piirin aktiivinen vastus on, sitä pienempi vaihesiirto virran ja jännitteen välillä.

Piirin tehonmuutoksen käyrä (katso kuva 3) kahdesti jakson aikana sai negatiivisen etumerkin, mikä, kuten jo tiedämme, on seurausta piirin reaktiivisuudesta. Mitä vähemmän reaktiivinen piiri, sitä pienempi vaihesiirto virran ja jännitteen välillä ja sitä enemmän virtalähdetehoa piiri kuluttaa.

Lue myös: Jänniteresonanssi