Jänniteresonanssi

Jos vaihtovirtapiiri on kytketty sarjaan induktori ja kondensaattori, niin ne vaikuttavat omalla tavallaan piiriä syöttävään generaattoriin sekä virran ja jännitteen välisiin vaihekytkennöihin.

Induktori saa aikaan vaihesiirron, jossa virta on neljänneksen jaksolla jäljessä jännitteestä, kun taas kondensaattori päinvastoin tekee piirin jännitteestä neljänneksen jakson jälkeen virtaa. Siten induktiivisen vastuksen vaikutus virran ja jännitteen väliseen vaihesiirtoon piirissä on päinvastainen kuin kapasitiivisen vastuksen vaikutus.

Tämä johtaa siihen, että kokonaisvaihesiirto virran ja jännitteen välillä piirissä riippuu induktiivisen ja kapasitiivisen vastusarvojen suhteesta.

Jos piirin kapasitiivisen resistanssin arvo on suurempi kuin induktiivisen, niin piiri on luonteeltaan kapasitiivinen, eli jännite on jäljessä vaihevirrasta. Jos päinvastoin piirin induktiivinen vastus on suurempi kuin kapasitiivinen, niin jännite johtaa virtaa ja siksi piiri on induktiivinen.

Tarkastelemamme piirin kokonaisreaktanssi Xtot määritetään lisäämällä käämin XL induktiivinen resistanssi ja kondensaattorin XC kapasitiivinen resistanssi.

Mutta koska näiden vastusten vaikutus piirissä on päinvastainen, yhdelle niistä, nimittäin Xc:lle, annetaan miinusmerkki, ja kokonaisreaktanssi määritetään kaavalla:

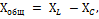
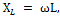
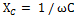
Käytä tätä piiriä Ohmin laki, saamme:

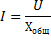
Tämä kaava voidaan muuntaa seuraavasti:

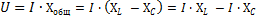
Tuloksena olevassa yhtälössä AzxL - piirin kokonaisjännitteen komponentin tehollinen arvo, joka voittaa piirin induktiivisen vastuksen, ja AzNSC - piirin kokonaisjännitteen komponentin tehollinen arvo, joka voittamaan kapasitiivisen vastuksen.

Näin ollen kelan ja kondensaattorin sarjakytkennästä koostuvan piirin kokonaisjännitteen voidaan katsoa koostuvan kahdesta termistä, joiden arvot riippuvat käämin induktiivisen ja kapasitiivisen vastuksen arvoista. piiri.

Uskoimme, että sellaisella piirillä ei ole aktiivista vastusta. Kuitenkin tapauksissa, joissa piirin aktiivinen vastus ei ole enää niin pieni, että se on merkityksetön, piirin kokonaisresistanssi määritetään seuraavalla kaavalla:

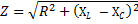
missä R on piirin aktiivinen kokonaisresistanssi, XL -NSC — sen kokonaisreaktanssi. Siirtyen Ohmin lain kaavaan, meillä on oikeus kirjoittaa:

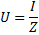
AC jännitteen resonanssi

Sarjaan kytketyt induktiiviset ja kapasitiiviset vastukset aiheuttavat vähemmän vaihesiirtoa virran ja jännitteen välillä vaihtovirtapiirissä kuin jos ne sisällytettäisiin piiriin erikseen.

Toisin sanoen näiden kahden luonteeltaan erilaisen reaktion samanaikaisesta toiminnasta piirissä tapahtuu vaihesiirron kompensointi (keskinäinen tuhoutuminen).

Täysi korvaus, ts. virran ja jännitteen välisen vaihesiirron täydellinen eliminointi tällaisessa piirissä tapahtuu, kun induktiivinen vastus on yhtä suuri kuin piirin kapasitiivinen vastus, eli kun XL = XC tai, mikä on sama, kun ωL = 1 / ωC.

Tässä tapauksessa piiri käyttäytyy puhtaasti aktiivisena vastuksena, eli ikään kuin siinä ei olisi käämiä eikä kondensaattoria. Tämän vastuksen arvo määräytyy kelan ja liitäntäjohtimien aktiivisten vastusten summasta. Jossa tehollinen virta piirissä on suurin ja määräytyy Ohmin lain kaavan I = U / R mukaan, missä Z on nyt korvattu R:llä.

Samanaikaisesti kelaan UL = AzxL ja kondensaattoriin Uc = AzNSCC vaikuttavat jännitteet ovat yhtä suuret ja mahdollisimman suuret. Kun piirin aktiivinen vastus on pieni, nämä jännitteet voivat moninkertaisesti ylittää piirin napojen kokonaisjännitteen U. Tätä mielenkiintoista ilmiötä kutsutaan sähkötekniikassa jänniteresonanssiksi.

Kuvassa Kuva 1 esittää jännitteiden, virtojen ja tehon käyriä resonanssijännitteillä piirissä.

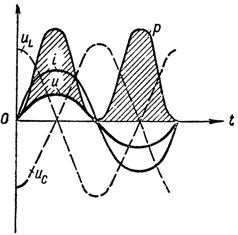
Kaavio jännitevirrasta ja tehosta jänniteresonanssissa

On syytä muistaa, että resistanssit XL ja C ovat muuttujia, jotka riippuvat virran taajuudesta ja kannattaa ainakin hieman muuttaa sen taajuutta, esimerkiksi kasvattaa sitä, koska XL = ωL kasvaa ja XSC = = 1 / ωC pienenee ja siten jänniteresonanssi piirissä häiriintyy välittömästi, kun taas aktiivisen resistanssin mukana reaktanssi ilmestyy piiriin. Sama tapahtuu, jos muutat piirin induktanssin tai kapasitanssin arvoa.

Jänniteresonanssilla virtalähteen teho käytetään vain piirin aktiivisen vastuksen voittamiseksi, eli johtojen lämmittämiseen.

Itse asiassa piirissä, jossa on yksi induktiivinen käämi, esiintyy energian vaihteluita, ts. säännöllinen energian siirto generaattorilta magneettikenttä kelat. Kondensaattorilla varustetussa piirissä tapahtuu sama asia, mutta kondensaattorin sähkökentän energian vuoksi. Piirissä, jossa on kondensaattori ja kela jänniteresonanssilla (ХL = XС), virta, kun virtapiiri on varastoinut, siirtyy määräajoin käämistä kondensaattoriin ja päinvastoin, ja vain energiankulutus, joka on tarpeen aktiivisen vastuksen voittamiseksi. piiri kuuluu osuuteen virtalähteestä. Siksi energianvaihto tapahtuu kondensaattorin ja kelan välillä lähes ilman generaattorin osallistumista.

Jänniteresonanssi on vain murrettava arvolla, kuinka käämin magneettikentän energia muuttuu eriarvoiseksi kondensaattorin sähkökentän energian kanssa, ja näiden kenttien välisessä energianvaihdossa syntyy ylimääräistä energiaa. ilmestyy, joka virtaa ajoittain ulos piirissä olevasta lähteestä ja syöttää sen sitten takaisin siihen piirissä.

Tämä ilmiö on hyvin samanlainen kuin mitä tapahtuu kellokoneistossa. Kellon heiluri pystyisi värähtelemään jatkuvasti ilman jousen (tai kellopyörän painon) apua, elleivät sen liikettä hidastavat kitkavoimat olisivat.

Jousi, välittämällä osan energiastaan ​​heiluriin oikealla hetkellä, auttaa sitä voittamaan kitkavoimat ja siten saavuttamaan värähtelyn jatkuvuuden.

Samoin sähköpiirissä, kun siinä esiintyy resonanssia, virtalähde kuluttaa energiansa vain voittaakseen piirin aktiivisen resistanssin, mikä auttaa siinä olevaa värähtelyprosessia.

Siten tulemme siihen tulokseen, että vaihtovirtapiiristä, joka koostuu generaattorista ja sarjaan kytketystä kelasta ja kondensaattorista, tulee tietyissä olosuhteissa XL = XС värähtelevä järjestelmä... Tätä piiriä kutsuttiin oskilloivaksi piiriksi.

Yhtälöstä XL = XС on mahdollista määrittää generaattorin taajuuden arvot, jolla jänniteresonanssiilmiö tapahtuu:

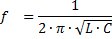
Merkitys kapasitanssi ja induktanssi piirissä, jossa jänniteresonanssi esiintyy:

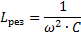
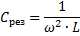
Siten muuttamalla mitä tahansa näistä kolmesta suuresta (eres, L ja C), on mahdollista aiheuttaa piiriin jänniteresonanssia eli muuttaa piiri värähteleväksi piiriksi.

Esimerkki hyödyllisestä jänniteresonanssin sovelluksesta: Vastaanottimen tulopiiriä säädetään säädettävällä kondensaattorilla (tai variometrillä) siten, että siinä esiintyy jänniteresonanssia. Tällä saavutetaan suuri lisäys normaaliin vastaanottimen toimintaan vaadittavaan kelajännitteeseen verrattuna antennin luomaan piirijännitteeseen.

Jänniteresonanssi-ilmiön hyödyllisen käytön ohella sähkötekniikassa on usein tapauksia, joissa jänniteresonanssi on haitallista.. Suuri jännitteen nousu piirin yksittäisissä osissa (käämessä tai kondensaattorissa) jännitteeseen verrattuna generaattorin vaurioituminen voi johtaa erillisten osien ja mittalaitteiden vaurioitumiseen.