Mikä on sähkönsyöttö?

Nykyihminen kohtaa jatkuvasti sähköä arjessa ja työssä, käyttää sähkövirtaa kuluttavia ja sitä tuottavia laitteita. Kun työskentelet heidän kanssaan, sinun tulee aina ottaa huomioon niiden teknisiin ominaisuuksiin liittyvät ominaisuudet.

Yksi minkä tahansa sähkölaitteen pääindikaattoreista on sellainen fyysinen määrä kuin sähköenergia... Sähkön tuotannon, siirron tai muuntamisen intensiteetiksi tai nopeudeksi on tapana kutsua muun tyyppistä energiaa, esimerkiksi lämpöä, valoa, mekaaninen.

Suuren sähköenergian kuljetus tai siirto teollisiin tarkoituksiin suoritetaan sen mukaisesti suurjännitejohtoja.

Muutos sähköenergiaa suoritetaan muuntaja-asemilla.

Sähköä kuluu kotitalouksien ja teollisuuden laitteissa eri tarkoituksiin. Yksi niiden yleisimmistä tyypeistä on hehkulamput eri luokituksilla.

Generaattorien, voimalinjojen ja kuluttajien sähköteholla tasa- ja vaihtovirtapiireissä on sama fyysinen merkitys, joka ilmaistaan ​​samanaikaisesti eri suhteissa yhdistelmäsignaalien muodosta riippuen. Yleisten mallien, hetkellisten arvojen käsitteiden määrittelemiseksi... Ne taas korostavat sähkön muuntumisnopeuden riippuvuutta ajasta.

Hetkellisen sähkötehon määritys

Teoreettisessa sähkötekniikassa virran, jännitteen ja tehon perussuhteiden johtamiseksi käytetään niiden kuvia hetkellisten arvojen muodossa, jotka ovat kiinteät tiettyyn ajankohtaan.

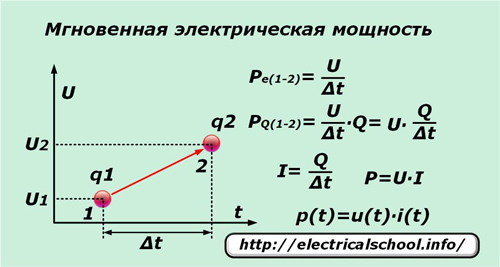
Jos hyvin lyhyessä ajassa ∆t yksi alkuainevaraus q siirtyy jännitteen U vaikutuksesta pisteestä «1» pisteeseen «2», niin se suorittaa näiden pisteiden välisen potentiaalieron verran työtä. Jakamalla se aikavälillä ∆t saadaan lauseke hetkelliselle teholle yksikkövarausta kohti Pe (1-2).

Koska ei vain yksittäinen varaus liikkuu käytetyn jännitteen vaikutuksesta, vaan myös kaikki vierekkäiset, jotka ovat tämän voiman vaikutuksen alaisia, joiden lukumäärää edustaa kätevästi numero Q, niin tehon PQ hetkellinen arvo (1-2) voidaan kirjoittaa heille.

Yksinkertaisten muunnosten suorittamisen jälkeen saadaan lauseke teholle P ja sen hetkellisen arvon p (t) riippuvuus hetkellisen virran i (t) ja jännitteen u (t) tulon komponenteista.

Vakiosähkötehon määritys

V DC-piirit jännitehäviön suuruus piiriosassa ja sen läpi kulkeva virta ei muutu ja pysyy vakaana, yhtä suurena kuin hetkelliset arvot.Siksi tämän piirin teho voidaan määrittää kertomalla nämä arvot tai jakamalla täydellinen työ A sen suoritusjaksolla, kuten selittävässä kuvassa näkyy.

Vaihtovirran sähkötehon määritys

Sähköverkkojen kautta siirrettyjen virtojen ja jännitteiden sinimuotoisen vaihtelun lait vaikuttavat tehon ilmaisuun tällaisissa piireissä. Tässä tulee peliin näennäinen teho, jota kuvataan tehokolmiolla ja joka koostuu aktiivisista ja reaktiivisista komponenteista.

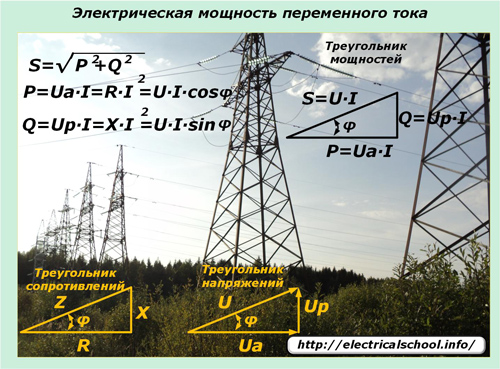
Sinimuotoinen sähkövirta kulkiessaan voimalinjojen läpi, joissa on sekakuormitus kaikissa osissa, ei muuta sen harmonisen muotoa ja jännitehäviö reaktiivisilla kuormilla siirtyy vaiheittain tiettyyn suuntaan. Momenttiarvolausekkeet auttavat ymmärtämään kohdistettujen kuormien vaikutusta piirin tehonmuutokseen ja sen suuntaan.

Samanaikaisesti kiinnitä välittömästi huomiota siihen, että virran suunta generaattorista kuluttajalle ja luodun piirin kautta lähetetty teho ovat täysin erilaisia ​​​​asioita, jotka joissakin tapauksissa eivät vain ole samat, vaan myös suunnattu vastakkaisiin suuntiin.

Harkitse näitä suhteita ihanteellisessa, puhtaassa ilmenemismuodossaan erityyppisille kuormille:

• aktiivinen;

• kapasitiivinen;

• induktiivinen.

Aktiivinen kuorman tehohäviö

Oletetaan, että generaattori tuottaa ihanteellisen sinimuotoisen jännitteen u, joka syötetään piirin puhtaasti aktiiviseen resistanssiin. Ampeerimittari A ja volttimittari V mittaavat virtaa I ja jännitettä U joka kerta t.

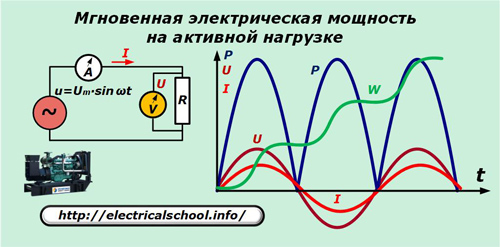
Kaavio osoittaa, että virran sinimuodot ja jännitehäviö aktiivisen resistanssin yli vastaavat taajuutta ja vaihetta, mikä aiheuttaa samat värähtelyt. Niiden tulon ilmaisema voima värähtelee kaksinkertaisella taajuudella ja pysyy aina positiivisena.

p = u ∙ i = Um ∙ sinωt ∙ Um / R ∙ sinωt = Um2/ R ∙ sin2ωt = Um2/ 2R ∙ (1-cos2ωt).

Jos mennään ilmaisuun käyttöjännite, niin saadaan: p = P ∙ (1-cos2ωt).

Integroimme sitten tehon yhden värähtelyn T ajanjaksolle ja voimme havaita, että energiavahvistus ∆W tällä aikavälillä kasvaa. Ajan myötä vastus kuluttaa edelleen uusia sähkön osia, kuten kaaviosta näkyy.

Reaktiivisilla kuormilla energiankulutuksen ominaisuudet ovat erilaiset, niillä on erilainen muoto.

Kapasitiivinen tehohäviö

Korvaa generaattorin sähköpiirissä resistiivinen elementti kondensaattorilla, jonka kapasitanssi on C.

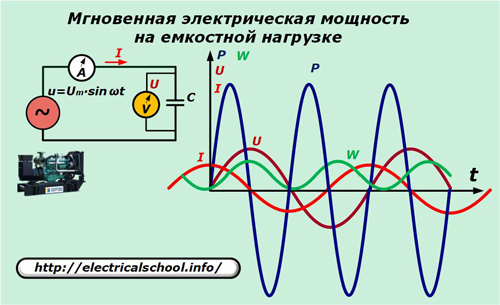
Virran ja kapasitanssin jännitehäviön välinen suhde ilmaistaan ​​suhteella: I = C ∙ dU / dt = ω ∙ C ∙ Um ∙ cosωt.

Kerrotaan virran hetkellisten ilmaisujen arvot jännitteellä ja saadaan kapasitiivisen kuorman kuluttaman tehon arvo.

p = u ∙ i = Um ∙ sinωt ∙ ωC ∙ Um ∙ cosωt = ω ∙ C ∙ Um2∙ sinωt ∙ cosωt = Um2/ (2X° C) ∙ Um2ψ2 (∙ sin2ω t = sin2ωt.

Tässä näkyy, että teho vaihtelee nollan ympärillä kaksinkertaisella jännitteen taajuudella. Sen kokonaisarvo harmoniselle jaksolle sekä energiavahvistukselle on nolla.

Tämä tarkoittaa, että energia liikkuu piirin suljettua piiriä pitkin molempiin suuntiin, mutta ei toimi.Tällainen tosiasia selittyy sillä, että kun lähdejännite kasvaa absoluuttisena arvona, teho on positiivinen ja energiavirta piirin läpi ohjataan säiliöön, jossa energiaa kertyy.

Kun jännite on siirtynyt putoavaan harmoniseen osaan, energia palautetaan kondensaattorista piiriin lähteeseen. Kummassakaan prosessissa ei tehdä hyödyllistä työtä.

Tehonhäviö induktiivisessa kuormassa

Vaihda nyt syöttöpiirissä kondensaattori induktanssilla L.

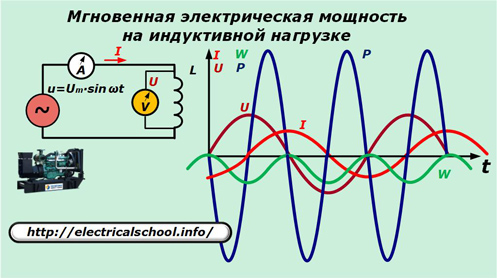
Tässä induktanssin läpi kulkeva virta ilmaistaan ​​suhteella:

I = 1 / L∫udt = -Um / ωL ∙ cos ωt.

Sitten saamme

p = u ∙ i = Um ∙ sinωt ∙ ωC ∙ (-Um / ωL ∙ cosωt) = — Um2/ ωL ∙ sinωt ∙ cosωt = -Um2/ (2ХL) ∙ -2 sinωt ∙ -2 sinωt

Tuloksena olevien lausekkeiden avulla voimme nähdä tehon suunnan muutoksen ja energian kasvun luonteen induktanssilla, joka suorittaa samat työnteon kannalta turhat värähtelyt kuin kapasitanssilla.

Loiskuormissa vapautuvaa tehoa kutsutaan loiskomponentiksi. Ihanteellisissa olosuhteissa, kun liitäntäjohdoilla ei ole aktiivista vastusta, se näyttää vaarattomalta eikä aiheuta haittaa. Mutta todellisissa tehoolosuhteissa jaksolliset transientit ja loistehon vaihtelut aiheuttavat kaikkien aktiivisten elementtien, mukaan lukien liitäntäjohtojen, kuumenemista, joihin kuluu jonkin verran energiaa ja lähteen käytetyn täyden tehon arvo laskee.

Suurin ero tehon loiskomponentin välillä on, että se ei tee lainkaan hyödyllistä työtä, vaan johtaa sähköenergian hävikkiin ja laitteiden ylikuormitukseen, mikä on erityisen vaarallista kriittisissä tilanteissa.

Näistä syistä loistehon vaikutuksen eliminoimiseksi mm teknisiä järjestelmiä sen korvaamiseksi.

Tehonjako sekakuormalla

Esimerkkinä käytetään generaattorin kuormaa, jolla on aktiivinen kapasitiivinen ominaisuus.

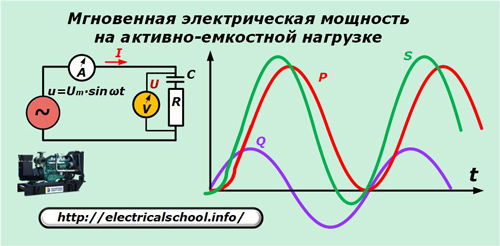
Kuvan yksinkertaistamiseksi virtojen ja jännitteiden sinimuotoja ei näytetä annetussa kaaviossa, mutta on pidettävä mielessä, että kuorman aktiivis-kapasitiivisessa luonteessa virtavektori johtaa jännitettä.

p = u ∙ i = Um ∙ sinωt ∙ ωC ∙ Im ∙ sin (ωt + φ).

Muutosten jälkeen saadaan: p = P ∙ (1- cos 2ωt) + Q ∙ sin2ωt.

Nämä kaksi termiä viimeisessä lausekkeessa ovat hetkellisen näennäistehon aktiiviset ja reaktiiviset komponentit. Vain ensimmäinen näistä tekee hyödyllistä työtä.

Tehonmittaustyökalut

Sähkön kulutuksen analysoimiseksi ja sen laskemiseksi käytetään mittalaitteita, joita on pitkään kutsuttu "Taskurit"… Heidän työnsä perustuu virran ja jännitteen tehollisten arvojen mittaamiseen ja niiden automaattiseen kertomiseen tiedon lähdöllä.

Mittarit näyttävät energiankulutuksen laskemalla sähkölaitteiden käyttöajan asteittain siitä hetkestä, kun mittari kytketään päälle kuormitettuna.

Tehon aktiivisen komponentin mittaamiseksi AC-piireissä, wattimetrit, ja reaktiiviset - varmetrit. Niillä on erilaiset yksikkönimet:

• watti (W, W);

• var (var, var, var).

Kokonaisenergiankulutuksen määrittämiseksi on tarpeen laskea sen arvo käyttämällä tehokolmiokaavaa wattimittarin ja varmittarin lukemien perusteella. Se ilmaistaan ​​omissa yksiköissään - volttiampeereissa.

Jokaisen yksikön hyväksytyt nimitykset auttavat sähköasentajia arvioimaan paitsi sen arvon, myös tehokomponentin luonteen.