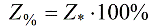Suhteellisten yksiköiden järjestelmä

Laskelmien yksinkertaistamiseksi parametreja laskettaessa tehonsiirtojärjestelmissä käytetään suhteellisten yksiköiden järjestelmää. Tämä menetelmä sisältää järjestelmän arvon nykyisen arvon ilmaisemisen yksikkönä otettuna perusarvona (perusarvona).

Suhteellinen arvo ilmaistaan ​​siis kertoimena perusarvosta (virta, jännite, vastus, teho jne.), eikä se ole suhteellisissa yksiköissä ilmaistuna riippuvainen jännitetasosta. Englanninkielisessä kirjallisuudessa suhteellisia yksiköitä merkitään pu tai p.u. (yksikköjärjestelmästä — suhteellisten yksiköiden järjestelmä).

Esimerkiksi samantyyppisillä muuntajilla jännitehäviö, impedanssi ja häviöt vaihtelevat absoluuttisesti eri jännitteillä. Mutta suhteellisessa koossa ne pysyvät suunnilleen samoina. Kun laskenta on tehty, tulokset muunnetaan helposti takaisin järjestelmäyksiköiksi (ampeereina, voltteina, ohmeina, watteina jne.), koska perusarvot, joihin virta-arvoja verrataan, ovat aluksi tiedossa.

Suhteelliset yksiköt ovat pääsääntöisesti käteviä siirrettävän tehon laskemiseen, mutta usein käy niin, että moottorigeneraattoreiden ja muuntajien parametrit määritellään suhteellisissa yksiköissä, joten jokaisen insinöörin tulisi tuntea suhteellisten yksiköiden käsite. Suhteellisessa yksikköjärjestelmässä käytetään tehon, virran, jännitteen, impedanssin ja sisäänpääsyn yksiköitä. Teho ja jännite ovat itsenäisiä suureita, jotka sanelevat todellisten energiajärjestelmien ominaisuudet.

Kaikki järjestelmän verkkoarvot voidaan ilmaista valittujen perusarvojen kerrannaisina. Joten jos puhumme tehosta, muuntajan nimellisteho voidaan valita perusarvoksi. Tapahtuu, että tietyllä hetkellä saatu teho suhteellisen arvon muodossa helpottaa suuresti laskelmia. Jännitteen perustana on nimellisväylän jännite jne.

Yleisesti ottaen konteksti antaa sinun aina ymmärtää, mistä suhteellisesta arvosta keskustellaan, ja edes saman symbolin "pu" läsnäolo englanninkielisessä kirjallisuudessa ei häiritse sinua.

Joten kaikki järjestelmän fyysiset suureet on nimetty. Mutta kun käännämme ne suhteellisiksi yksiköiksi (todellisuudessa prosentteina), teoreettisten laskelmien luonne yleistyy.

Jonkin fysikaalisen suuren suhteellinen arvo ymmärretään sen suhteena johonkin perusarvoon, eli arvoon, joka on valittu yksiköksi tietylle mittaukselle. Suhteellinen arvo on merkitty alla tähdellä.

Usein laskelmissa otetaan seuraavat perusarvot: perusvastus, perusvirta, perusjännite ja perusteho.

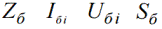
Alaindeksi «b» osoittaa, että tämä on perusarvo.

Sitten suhteellisia mittayksiköitä kutsutaan suhteelliseksi perusarvoksi:

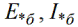
Tähti osoittaa suhteellista arvoa, kirjain «b» - perustaa. EMF on suhteellisen perustavanlaatuinen, virta suhteellisen perustavanlaatuinen jne. Ja suhteelliset perusyksiköt määritetään seuraavilla lausekkeilla:

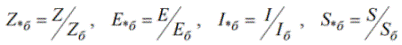
Esimerkiksi kulmanopeuksien mittaamiseksi kulmasynkroninen nopeus otetaan yksikkönä ja siksi synkroninen kulmanopeus on yhtä suuri kuin peruskulmanopeus.

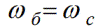
Sitten mielivaltainen kulmanopeus voidaan ilmaista suhteellisissa yksiköissä:

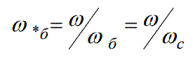
Näin ollen seuraavia suhteita voidaan pitää perusvuon kytkennälle ja induktiivuudelle:

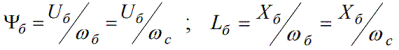
Tässä päävuon sidos on vuosidos, joka indusoi pääjännityksen pääkulmanopeudella.

Joten, jos synkroninen kulmanopeus otetaan perustaksi, niin:

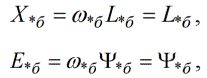
suhteellisissa yksiköissä emf on yhtä suuri kuin vuo ja induktiivinen vastus on yhtä suuri kuin induktanssi. Tämä johtuu siitä, että perusyksiköt on valittu asianmukaisesti.

Harkitse sitten vaihejännitettä suhteellisissa ja perusyksiköissä:

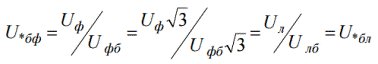
On helppo nähdä, että vaihejännite suhteellisissa perusyksiköissä on yhtä suuri kuin lineaarinen suhteellinen perusjännite. Vastaavasti jännitysamplitudin arvo suhteellisissa yksiköissä osoittautuu yhtä suureksi kuin tehollinen:

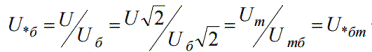
Näistä riippuvuuksista käy ilmi, että suhteellisissa yksiköissä jopa kolmen vaiheen teho ja yhden vaiheen teho ovat yhtä suuret, ja generaattorin herätevirrat, -vuot ja emf - osoittautuvat myös keskenään yhtä suuriksi.

Tässä on tärkeää huomata, että kunkin piirin elementin suhteellinen resistanssi on yhtä suuri kuin suhteellinen jännitehäviö piiriin syötetyn nimellistehon olosuhteissa.

Oikosulkuvirtoja laskettaessa käytetään neljää pääparametria: virta, jännite, vastus ja teho. Jännitteen ja tehon perusarvot pidetään itsenäisinä, ja niiden kautta ilmaistaan ​​perusvastus ja -virta. Kolmivaiheisen verkon tehoyhtälöstä - virta siis Ohmin laki - vastus:

Koska perusarvo voidaan valita mielivaltaisesti, samalla fyysisellä suurella voi suhteellisissa yksiköissä ilmaistuna olla erilaiset numeeriset arvot. Siksi generaattoreiden, moottoreiden ja muuntajien suhteelliset resistanssit asetetaan suhteellisissa yksiköissä syöttämällä suhteelliset nimellisyksiköt. Sn - nimellisteho. Un — nimellisjännite. Suhteelliset nimellisarvot kirjoitetaan indeksillä «n»:

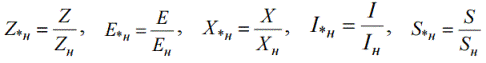
Nimellisresistanssien ja -virtojen löytämiseksi käytetään vakiokaavoja:

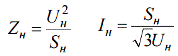
Suhteellisten yksiköiden ja nimettyjen määrien välisen suhteen määrittämiseksi ilmaisemme ensin suhteellisen kantaluvun ja perussuureiden välisen suhteen:

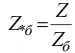
Kirjoitetaan perusresistanssi tehon ja korvikkeen suhteen:

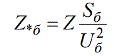
Joten voit muuntaa määritetyn arvon suhteelliseksi perusarvoksi.

Ja samalla tavalla voit luoda suhteen suhteellisten nimellisten yksiköiden ja substantiivien välille:

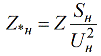
Laske vastus nimetyissä yksiköissä tunnetuilla suhteellisilla nimellisarvoilla käyttämällä seuraavaa kaavaa:

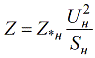
Suhteellisten nimellisyksiköiden ja suhteellisten perusyksiköiden välinen suhde määritetään seuraavalla kaavalla:

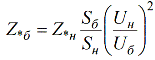
Tätä kaavaa käyttämällä suhteelliset nimellisyksiköt voidaan muuntaa suhteellisiksi perusyksiköiksi.

Sähköjärjestelmissä oikosulkuvirtojen rajoittamiseksi aseta nykyiset rajoitetut reaktorit, itse asiassa - lineaariset kelat. Ne saavat nimellisjännitteen ja -virran, mutta eivät tehoa.

Olettaen että

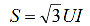
ja muuttamalla yllä olevat lausekkeet suhteelliselle nimellis- ja suhteelliselle kantaresistanssille, saamme:

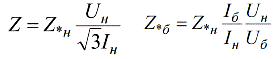
Suhteelliset arvot voidaan ilmaista prosentteina: