Piiritopologiat – peruskäsitteet

Sähköpiiri on joukko laitteita (elementtejä) ja niiden liitäntäjohtoja, joiden läpi sähkövirta voi kulkea. Kaikki sähköpiirien elementit ovat yhteisiä passiivisessa ja aktiivisessa.

Aktiiviset elementit muuttavat erilaisia ​​energiatyyppejä (mekaaninen, kemiallinen, valo jne.) sähköenergiaksi. Passiivisissa laitteissa sähköenergia muunnetaan muun tyyppiseksi energiaksi. Aktiivisia elementtejä kutsutaan lähteiksi, passiivisia kutsutaan kuluttajiksi tai vastaanottimiksi.

Piiriteoriassa tarkastellaan sähköisten elementtien idealisoituja malleja. Tämä tekee elementtien kuvauksesta mahdollisimman yksinkertaista. Monimutkaisemmat, todelliset elementit mallinnetaan idealisoitujen elementtien joukosta.

Sähköpiirien tärkeimmät passiiviset elementit ovat vastus (resistiivinen elementti), induktori (induktiivinen elementti) ja kondensaattori (kapasitiivinen elementti). Elementit asennetaan sähköpiiriin tuottamaan tietyn arvon ja muodon jännite ja virta (katso - Sähköpiiri ja sen elementit).

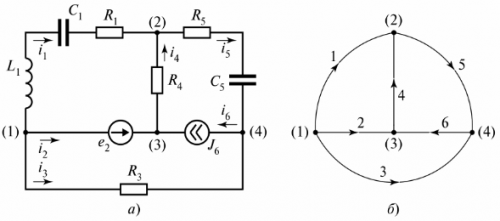
Sähköpiiri koostuu haaroista ja solmuista. Haara — tämä on sähköpiirin (piirin) osa, jonka läpi kulkee sama virta. solmu — kolmen tai useamman haaran yhdistäminen. Sähkökaaviossa solmu on merkitty pisteellä (kuva 1).

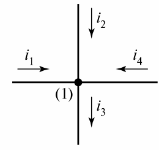
Riisi. 1. Määrittele solmu kaaviossa

Tarvittaessa kaavion solmut numeroidaan vasemmalta oikealle ylhäältä alas.

Kuvassa Kuvassa 2 on esitetty resistiivis-kapasitiivinen haara, jossa virta iC kulkee.

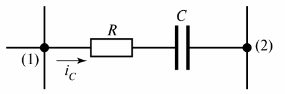
Riisi. 2. Resistiivis-kapasitiivinen haara

Toinen haaran määritelmä voidaan antaa - se on piirin osa kahden vierekkäisen solmun välillä (solmut (1) ja (2) kuvassa 2).

Ketju Onko sähköpiirissä suljettu polku? Piiri voidaan sulkea millä tahansa haaralla, mukaan lukien ehdolliset haarat, joiden resistanssi on yhtä suuri kuin ääretön.

Kuvassa Kuva 3 esittää haarautunutta sähköpiiriä, joka koostuu kolmesta haarasta.

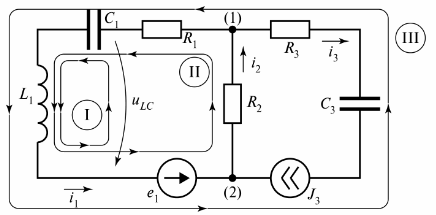
Riisi. 3. Sähköpiiri kahdella piirillä

Kaavio esittää kolme piiriä, ja piiri I on suljettu äärettömän vastuksen haaralla. Tämä haara on merkitty jännitteellä tiLC.

Kuvan piirille. 3 on mahdollista muodostaa monia silmukoita, jotka suljetaan todellisilla tai ehdollisilla haaroilla, mutta sähköisen kohinan laskemiseen käytetään käsitettä "itsenäinen silmukka". Riippumattomien piirisilmukoiden lukumäärä asetetaan aina laskennassa vaadittavaksi vähimmäismääräksi.

Itsenäiset piirit ovat aina suljettuja, mutta haarat, joiden resistanssi ei ole yhtä suuri kuin ääretön, ja jokainen riippumaton piiri sisältää vähintään yhden haaran, joka ei sisälly muihin piireihin. Monimutkaisissa sähköpiireissä voit määrittää riippumattomien piirien lukumäärän piirikaavion avulla.

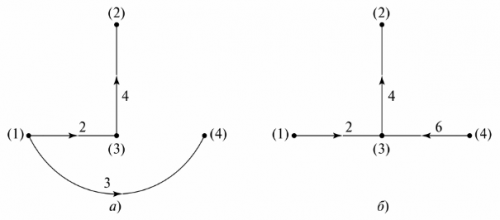
Kytkentäkaaviossa kutsutaan piirin ehdollista esitystä, jossa jokainen haara korvataan linjasegmentillä. Haaroissa olevia kohteita ei näytetä. Esimerkiksi kuviossa 10 2000-2000 on esitetty Kuva 4 esittää haarapiirin ja sen kaavion.

Riisi. 4. Haaroittunut sähköpiiri: a — kytkentäkaavio, b — kaavio

Kaavion kaavion tekemiseksi solmut on yhdistettävä haaralinjoilla ilman, että niissä määritetään elementtejä. Haarat on numeroitu ja niissä olevien virtojen suunnat on merkitty nuolilla. Graafilla itsessään ei ole fyysistä merkitystä, mutta sitä voidaan käyttää itsenäisten ääriviivojen lukumäärän ja tyypin määrittämiseen. Tätä tarkoitusta varten valmistetaan "graafinen puu".

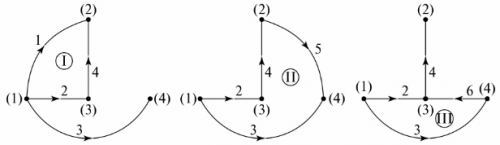
Graafinen puu Se edustaa kaaviota piiristä, jonka solmut on yhdistetty haaroilla siten, ettei tuloksena ole suljettua silmukkaa. Graafisen puun näyttämiseen voi olla useita vaihtoehtoja. Kuvassa Kuvio 5 esittää kahta mahdollista vaihtoehtoa kuvion 1 piirille. 4.

Riisi. 5. Kaavan graafinen puu

Graafipuussa puuttuvien haarojen määrä on yhtä suuri kuin piirin itsenäisten silmukoiden lukumäärä. Esimerkissä nämä ovat kolme haaraa, kolme itsenäistä silmukkaa. Riippumattomien silmukoiden konfiguraatio voidaan saada yhdistämällä graafipuun solmut peräkkäin haaroihin, joita ei ole määritetty graafipuussa. Esimerkiksi kuvion kaaviopuulle. Kuviossa 5 on esitetty itsenäiset ääriviivat. 6.

Riisi. 6. Riippumattomien ääriviivojen määrittäminen kuvaajapuun avulla

Vaihtoehto riippumattomien piirien konfiguroimiseksi piirin laskemista varten tehdään piirianalyysin aikana. Sellaiset ääriviivat tulee valita niin, että laskenta on mahdollisimman yksinkertaista, ts. riippuvien yhtälöiden määrä järjestelmässä on minimaalinen.

Topologiset yhtälöt muodostavat suhteen jännitteiden ja virtojen välille piirissä, ja yhtälöiden lukumäärä ja tyyppi eivät riipu siitä, mitkä elementit ovat mukana haaroissa. Topologiset yhtälöt sisältävät yhtälöt, jotka koostuvat Kirchhoffin lakien mukaan.