Tehosuhde yksinkertaisimmassa sähköpiirissä

Tässä artikkelissa ymmärrämme, mikä lähteen ja vastaanottimen parametrien suhteen tulisi olla, jotta saavutetaan sähköpiirin optimaalinen toimintatapa. Tehosuhteet ovat tärkeitä myös pienivirtateknologioissa. Periaatteessa näihin kysymyksiin voidaan vastata esimerkin avulla yksinkertaisin sähköpiiri.

Piiri koostuu tasavirtalähteestä, jossa on EMF E ja sisäinen resistanssi Rwatt, joka tuottaa sähköenergiaa, ja vastaanottoenergian vastaanottimesta kuormitusresistanssilla Rn.

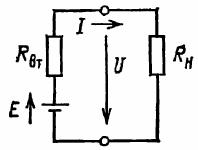
Riisi. 1. Kaavio, joka selittää tehosuhteen yksinkertaisimmassa piirissä

Koska lähteellä on sisäinen vastus, osa sen kehittämästä sähköenergiasta muunnetaan itse lämpöenergiaksi.

Kuvassa esitetyn piirin virta. 1

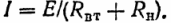
Tämän yhtälön perusteella määritämme vastaanottimen tehon (teho muuntaa sähköenergiaa muun tyyppisiksi):

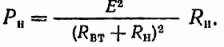
Samoin lähteen tehohäviöt:

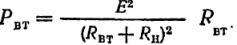
Lähteen sähkötehon tulee olla yhtä suuri kuin lähteessä ja vastaanottimessa muun tyyppisiksi muunnettujen tehojen summa, ts. on oltava tehotasapaino (kuten kaikissa piireissä):

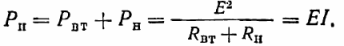
Päätejännite U voidaan myös syöttää tehon Pn lausekkeeseen.

Vastaanottimen teho:

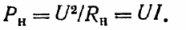
Suorituskykykerroin (COP), joka määritellään vastaanottimen tehon (hyödyllisen) suhteeksi kehitettyyn tehoon:

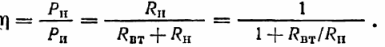
Yhtälö osoittaa, että tehokkuus riippuu kuormitusvastuksen suhteesta sisäiseen vastukseen. Näiden vastusten arvot ovat määräävä tekijä lähteen kehittämän tehon jakautumisessa:

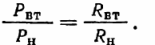
Tehoa Pn tulee pitää hyödyllisenä, lähteen Pvt tehohäviöt määräävät vain lähteen lämmityksen ja siksi vastaava energia kuluu tuottamatta.

Tehokkuus kasvaa Rn / Rvt -suhteen kasvaessa.

Suuren hyötysuhdearvon saamiseksi tulee suhde Pn> Pwt täyttyä, eli piirin on toimittava tilassa, joka on lähellä lähteen lepotilaan.

Käytännössä voidaan asettaa kaksi eri tehosuhdevaatimusta: korkea hyötysuhde ja tehonsovitus. Korkean hyötysuhteen vaatimus asetetaan esimerkiksi silloin, kun on tarpeen siirtää suuri määrä energiaa johtoja pitkin tai muuntaa tämä energia sähkökoneiksi. Pienikin tehokkuuden lisäys tuottaa tällaisissa tapauksissa suuria säästöjä.

Koska suurten energioiden käyttö on pääasiassa ominaista suurten virtojen tekniikalle, tällä alalla on tarpeen työskennellä lähellä joutokäyntitilaa.Lisäksi käytettäessä tällaisissa tiloissa päätejännite eroaa vain vähän lähteestä emf.

Pienvirtatekniikassa (erityisesti viestintätekniikassa ja mittaustekniikassa) käytetään erittäin pieniä teholähteitä, joissa on lisäksi suuria sisäinen vastus… Tällaisissa tapauksissa tehonsiirtoprosessia kuvaavalla tehokkuudella on usein toissijainen merkitys, ja vaatimus vastaanottimen vastaanottaman tehon suurimmasta mahdollisesta arvosta korostuu.

Kun suurvirtatekniikassa hyödyttömiä tai jopa haitallisia energian muunnoksia - energiahäviöitä pienennetään tehokkuuden kasvaessa, niin pienvirtatekniikassa kasvien ja laitteiden käytön tehokkuutta lisätään sähköpiirien tehojen oikealla koordinoinnilla.

Edellytys suurimman mahdollisen vastaanottimen tehon Pvmax saamiseksi lähteestä, jossa on EMF- ja sisäinen vastustiedot:

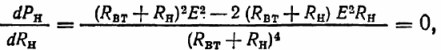
Tästä seuraa, että vastaanottimen maksimitehon ehto täyttyy yhtälöllä Rn = RВt

Siten, kun vastaanottimen resistanssit ja lähteen sisäinen resistanssi ovat samat, vastaanottimen vastaanottama teho on maksimi.

Jos Rn = Rw, niin

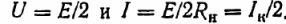
Vastaanottimen vastaanottamaa tehoa varten meillä on:

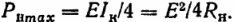
Esimerkki. Avulla lämpösähköinen muunnin (lämpöparit) sisäisellä resistanssilla Rw = 5 ohmia, saat jännitteen 0,05 mV / ° C. Suurin lämpötilaero on 200 ° C. Mitä sähköisiä tietoja osoittavalla sähkölaitteella tulisi olla (vastus, teho, virta), jos se haluaa saada maksimiteho muuntimesta.

Anna ratkaisu kahteen tapaukseen:

a) laite on kytketty suoraan muuntimeen;

b) laite on kytketty kahdella kuparilangalla, joiden pituus on l= 1000 m ja joiden poikkipinta-ala on C = 1 mm2.

Vastaus. Suurin jännite lämpösähköisen muuntimen liittimissä on yhtä suuri kuin sen EMF E = 200 * 0,05 = 10 mV.

Tässä tapauksessa piiriin liitetyn laitteen indikaattorin tulee olla maksimi (mittauksen ylärajalla).

a) Jotta laitteen teho olisi maksimaalinen, laitteen ja muuntimen resistanssit on sovitettava yhteen. Tätä tarkoitusta varten valitsemme laitteen resistanssin, joka vastaa termoparin vastusta, ts. Rn = Rt = 5 ohmia.

Löydämme laitteen suurimman tehon:

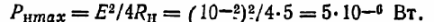
Määritä virta:

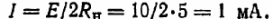
b) Jos johtimien resistanssia ei voida jättää huomiotta, se on otettava huomioon määritettäessä lämpöparista ja kahdesta johtimesta koostuvan aktiivisen kaksinapaisen laitteen sisäistä kokonaisresistanssia, koska muuten vastaanottimen ja johdon välillä on epäsopivuus. lähde tehon suhteen.

Etsitään johtimien resistanssi, koska ominaisvastus on 0,0178 μOhm-m:

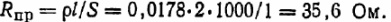
Siten laitteen vaadittu vastustaso on:

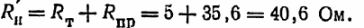
Tällä sisäisen vastuksen arvolla laitteen teho on suurin

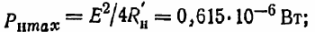
Piirivirta:

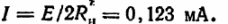
Saadut tulokset osoittavat, että on suositeltavaa valita lähteet, joiden sisäinen vastus on pieni, ja liitäntäjohtojen poikkipinta-alan tulee olla riittävän suuri.

Hyvin usein tällaisia ​​mittauksia suoritettaessa vastaanottimen ja lähteen yhteensopivuus lasketaan siihen, että käytettävissä olevista laitteista valitaan se, joka tietylle tai tunnetulle mitatun arvon maksimiarvolle saa suurimman. nuolen taipuminen ja tarjoaa siksi suurimman mittakaavan lukutarkkuuden.