Epälineaariset sähköpiirit
Epälineaaristen elementtien tarkoitus sähköpiireissä
V sähköpiirit voi sisältää passiivisia elementtejä, sähköinen vastus joka riippuu olennaisesti virrasta tai jännityksestä, jolloin virta ei ole suoraan verrannollinen jännitteeseen. Tällaisia elementtejä ja sähköpiirejä, joihin ne tulevat, kutsutaan epälineaariseksi elementiksi.
Epälineaariset elementit antavat sähköpiireille ominaisuuksia, joita ei voida saavuttaa lineaarisissa piireissä (jännitteen tai virran stabilointi, tasavirtavahvistus jne.). Ne ovat hallitsemattomia ja ohjattavia... Ensimmäinen — bipolaarinen — on suunniteltu toimimaan ilman ohjaustekijän vaikutusta niihin (puolijohdetermistorit ja -diodit), ja toista — moninapaista — käytetään, kun ohjaustekijä vaikuttaa niihin (transistorit). ja tyristorit).
Epälineaaristen elementtien virta-jännite-ominaisuudet
Epälineaaristen elementtien sähköiset ominaisuudet ovat kokeellisesti saatuja virta-jännite-ominaisuuksien I (U) käyriä, jotka osoittavat virran riippuvuuden jännitteestä, joille joskus tehdään likimääräinen, laskennallisesti kätevä empiirinen kaava.
Ohjaamattomilla epälineaarisilla elementeillä on yksi virta-jännite-ominaisuus, ja ohjatuilla epälineaarisilla elementeillä on perhe sellaisia ominaisuuksia, joiden parametri on ohjaava tekijä.
Lineaarisilla elementeillä on vakio sähkövastus, joten niiden virta-jännite-ominaisuus on origon kautta kulkeva suora viiva (kuva 1, a).
Epälineaarisen virta-jännite-ominaisuudet ovat eri muotoisia ja jaetaan symmetrisiin ja epäsymmetrisiin koordinaattiakseleiden suhteen (kuva 1, b, c).
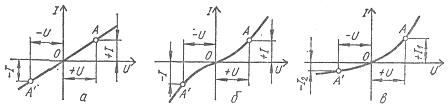
Riisi. 1. Passiivielementtien virta-jänniteominaisuudet: a — lineaarinen, b — epälineaarinen symmetrinen, c — epälineaarinen epäsymmetrinen
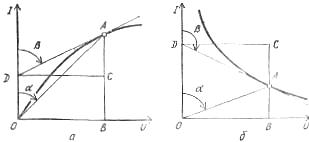
Riisi. 2. Kaaviot epälineaaristen elementtien staattisen differentiaalivastuksen määrittämiseksi virta-jännite-ominaisuuksien osissa: a — nousu, b — lasku
Epälineaarisilla elementeillä, joilla on symmetrinen virta-jännite-ominaisuus tai symmetrisillä elementeillä, jännitteen suunnan muutos ei aiheuta muutosta virran arvossa (kuva 1, b), ja epälineaarisissa elementeissä, joiden jännite on epäsymmetrinen. -virtakäyrä tai epäsymmetrisillä elementeillä, kun jännitteen itseisarvo on sama vastakkaisiin suuntiin, virrat ovat erilaisia (kuva 1, c). Siksi DC- ja AC-piireissä käytetään epälineaarisia symmetrisiä elementtejä ja AC-piireissä pääsääntöisesti epälineaarisia symmetrisiä elementtejä AC:n muuntamiseksi tasavirraksi.
Epälineaaristen elementtien ominaisuudet
Jokaiselle epälineaariselle elementille erotetaan staattinen resistanssi, joka vastaa tiettyä virta-jännite-ominaisuuden pistettä, esimerkiksi piste A:
Rst = U/I = muOB/miBA = mr tga
ja erovastus, joka on tarkoitettu. sama piste A määritetään kaavalla:
Rdiff = dU / dI = muDC / miCA = mr tgβ,
missä mi, mi, sir – vastaavasti jännitteiden, virtojen ja vastusten asteikko.
Staattinen vastus kuvaa epälineaarisen elementin ominaisuuksia vakiovirtatilassa ja differentiaaliresistanssi - virran pienille poikkeamille vakaan tilan arvosta. Molemmat muuttuvat siirtyessään pisteestä toiseen, joista ensimmäinen on aina positiivinen ja toinen muuttuja: ominaisuuden nousevassa osassa virtajännite on positiivinen ja laskevassa osassa negatiivinen.
Epälineaarisille elementeille on tunnusomaista myös käänteisarvot: staattinen johtavuus Gst ja differentiaalinen johtavuus G eri tai dimensiottomat parametrit —
suhteellinen vastus:
Kr = — (R-ero /Rst)
tai suhteellinen johtavuus:
Kg = — (G-ero / Gst)
Lineaaristen elementtien parametrit Kr ja Kilogram ovat yhtä suuret kuin yksi, ja epälineaarisilla elementeillä ne eroavat siitä, ja mitä enemmän ne eroavat yhdestä, sitä enemmän sähköpiirin epälineaarisuus ilmenee.
 Epälineaaristen sähköpiirien laskenta
Epälineaaristen sähköpiirien laskenta
Epälineaariset sähköpiirit lasketaan graafisesti ja analyyttisesti perustuen Kirchhoffin lait ja vaihtovirtapiirien yksittäisten elementtien voltti-ampeeriominaisuudet vaihtovirran muuntamiseksi tasavirraksi.
Kun lasketaan graafisesti sähköpiiri, jossa on kaksi sarjaan kytkettyä epälineaarista vastusta R1 ja R2, joiden virta-jännite-ominaisuudet Iz (U1) ja Iz (U2), rakenna koko piirin Iz (U) virta-jänniteominaisuus, jossa U = U1 + U2, jonka pisteiden abskissat saadaan laskemalla yhteen epälineaaristen vastusten virta-jännite-ominaisuuksien pisteiden abskissat, joilla on samat ordinaatit (kuva 3, a, b).
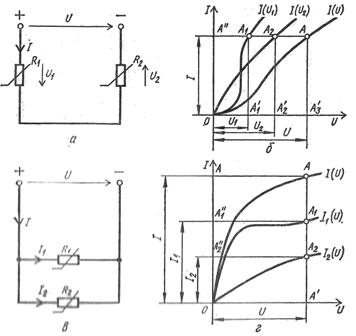
Riisi. 3. Epälineaaristen sähköpiirien kaaviot ja ominaisuudet: a — epälineaaristen vastusten sarjakytkentäpiiri, b — yksittäisten elementtien ja sarjapiirin volttiampeeriominaisuudet, c — epälineaaristen vastusten rinnakkaiskytkentäkaavio, d — yksittäisten elementtien ja rinnakkaispiirin jännite-ampeeriominaisuudet.
Tämän käyrän läsnäolo sallii jännitteen U löytää virran Az sekä jännitteen U1 ja U2 vastusten navoissa.
Samalla tavalla suoritetaan sähköpiirin laskenta, jossa on kaksi rinnakkain kytkettyä vastusta. R1 ja R2 virta-jännite-ominaiskäyrillä I1 (U) ja Az2 (U), joille rakennettiin koko piirin virta-jännite-ominaiskäyrä Az(U), missä Az = I1+I2, jolle tietyllä jännitteellä U, etsi virrat Az , I1, I2 (oris. 3, c, d).
Analyyttinen menetelmä epälineaaristen sähköpiirien laskemiseksi perustuu epälineaaristen elementtien jänniteominaisuuksien esittämiseen vastaavien matemaattisten funktioiden yhtälöiden kautta, joiden avulla voidaan laatia tarvittavat tilayhtälöt sähköpiireille. .Koska tällaisten epälineaaristen yhtälöiden ratkaiseminen aiheuttaa usein merkittäviä vaikeuksia, analyyttinen menetelmä epälineaaristen piirien laskemiseksi on kätevä, kun epälineaaristen elementtien virta-jännite-ominaisuuksien toiminta-osuudet voidaan oikaista. Tämän avulla voit kuvata piirin sähköistä tilaa lineaarisilla yhtälöillä, jotka eivät aiheuta vaikeuksia niiden ratkaisemisessa.
Sähkötekniikan perusteet:
Potentiaalierosta, sähkömotorisesta voimasta ja jännitteestä
Sähkövirta nesteissä ja kaasuissa
Tietoja magneettikentästä, solenoideista ja sähkömagneeteista
Itseinduktio ja keskinäinen induktio
Sähkökenttä, sähköstaattinen induktio, kapasitanssi ja kondensaattorit
Mikä on vaihtovirta ja miten se eroaa tasavirrasta

