Nykyinen tiheys

Kutsutaan arvoa, joka on yhtä suuri kuin virran suhde johtimen S virrantiheyden poikkipinta-alaan (nimitys δ).

Virran tiheys voidaan määrittää seuraavasti:

δ = I/S

Tässä tapauksessa oletetaan, että virta jakautuu tasaisesti langan poikkileikkaukselle. Johtojen virrantiheys mitataan yleensä yksikössä a / mm2.

Virran tiheys on vektorisuure. Virran tiheysvektori ja energialähteitä ja kuluttajia yhdistävät johdot on suunnattu normaalisti johtimen poikkipinta-alaan nähden.

Haaroittamattomassa sähköpiirissä virralla ja johtimien eri poikkileikkauksilla virrantiheydellä johtojen eri poikkileikkauksissa on sama arvo.

Jos oletetaan, että tasavirran suuruus osissa S1 ja C2 ei ole sama (kuva 1), niin poikkileikkausten S1 ja S2 läpi aikayksikköä kohti kulkevat varaukset olisivat erilaisia. Tämän seurauksena positiivinen tai negatiivinen varaus muodostuisi johtimen tilavuuteen näiden osien väliin. Tasavirralla tapahtuisi ääretön varausten kertyminen, mikä on mahdotonta tasavirralla.

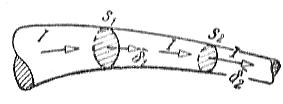
Riisi. 1. Sähkövirta ja virrantiheys haarautumattoman sähköpiirin eri osissa.

Virran tiheys johtimen S1 ja S2 poikkileikkauksen eri alueilla ei ole sama:

81 = I/S1, 82 = I/S2. Kun S1> S2, saamme δ1 δ2