Pienten ja suurten vastusten mittauksen ominaisuudet

Vastus on yksi tärkeimmistä parametreista virtapiiriminkä tahansa piirin tai asennuksen toiminnan määrittäminen.

Tiettyjen vastusarvojen saaminen sähkökoneiden, -laitteiden, -laitteiden valmistuksessa sähköasennusten asennuksen ja käytön aikana on edellytys niiden normaalin toiminnan varmistamiseksi.

Jotkut vastukset säilyttävät arvonsa käytännössä ennallaan, kun taas toiset päinvastoin ovat erittäin herkkiä ajoittain vaihteluille lämpötilan, kosteuden, mekaanisen rasituksen jne. vuoksi. Siksi sekä sähkökoneiden, -laitteiden, -laitteiden ja -laitteiden valmistuksessa että in Asennuksen aikana sähköasennusten on väistämättä mitattava vastus.

Resistanssimittausten tekemisen ehdot ja vaatimukset ovat hyvin erilaisia. Joissakin tapauksissa vaaditaan suurta tarkkuutta, toisissa päinvastoin riittää, että löydetään likimääräinen vastuksen arvo.

Arvosta riippuen sähkövastukset on jaettu kolmeen ryhmään:

• 1 ohm tai vähemmän - pieni vastus,

• 1 ohm - 0,1 Mohm - keskivastukset,

• 0,1 Mohm ja enemmän - korkea vastus.

Matalaa vastusta mitattaessa on ryhdyttävä toimenpiteisiin, joilla eliminoidaan vaikutus kytkentäjohtojen, koskettimien ja termo-EMF:n vastuksen mittaustulokseen.

Keskimääräisiä resistanssia mitattaessa voit jättää huomioimatta kytkentäjohtojen ja koskettimien resistanssit, voit jättää huomioimatta eristysvastuksen vaikutuksen.

Suuria vastuksia mitattaessa on otettava huomioon tilavuuden ja pinnan vastus, lämpötilan, kosteuden ja muiden tekijöiden vaikutus.

Matala vastuksen mittausominaisuudet

Pienten vastusten ryhmään kuuluvat: sähkökoneiden ankkurikäämit, ampeerimittareiden resistanssit, shuntit, virtamuuntajien käämien vastukset, väylän oikosulkujohtimien resistanssit jne.

Matalaresistanssia mitattaessa tulee aina ottaa huomioon mahdollisuus, että liitäntäjohtojen resistanssi ja transienttivastukset voivat vaikuttaa mittaustulokseen.

Testijohdon resistanssit ovat 1 x 104 - 1 x 102 ohm, liitosresistanssi - 1 x 105 - 1 x 102 ohm

Ohimenevällä vastuksella tai kosketusvastukset ymmärtää vastukset, joita sähkövirta kohtaa siirtyessään johdosta toiseen.

Ohimenevät vastukset riippuvat kosketuspinnan koosta, sen luonteesta ja kunnosta - sileä tai karkea, puhdas tai likainen, sekä kosketustiheydestä, puristusvoimasta jne.Ymmärretään esimerkin avulla siirtymäresistanssien ja kytkentäjohtojen vastusten vaikutus mittaustulokseen.

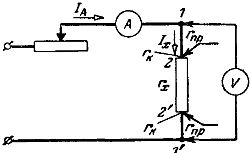
Kuvassa Kuva 1 on kaavio resistanssin mittaamisesta esimerkkiampeeri- ja volttimittarilla.

Riisi. 1. Väärä kytkentäkaavio matalan vastuksen mittaamiseen ampeeri- ja volttimittarilla.

Sano tarvittava resistanssi rx — 0,1 ohm ja volttimittarin vastus rv = 500 ohmia. Koska ne on kytketty rinnan, niin rNS/ rv= Iv / Ix = 0, 1/500 = 0,0002, eli volttimittarin virta on 0,02 % halutun resistanssin virrasta. Siten 0,02 %:n tarkkuudella ampeerimittarin virtaa voidaan pitää yhtä suurena kuin vaaditun resistanssin virta.

Jakamalla ampeerimittarin lukeman pisteisiin 1, 1′ kytketyn volttimittarin lukemat saadaan: U'v / Ia = r'x = rNS + 2рNS + 2рk, missä r'x on vaaditun vastuksen löydetty arvo ; rpr on liitäntäjohdon vastus; gk - kosketusvastus.

Ottaen huomioon rNS =rk = 0,01 ohm, saadaan mittaustulos r'x = 0,14 ohm, josta liitäntäjohtojen resistanssien ja kosketusresistanssien aiheuttama mittausvirhe on 40 % — ((0,14 — 0 .1) / 0,1 )) x 100 %.

On tarpeen kiinnittää huomiota siihen, että vaaditun vastuksen pienentyessä yllä mainituista syistä johtuva mittausvirhe kasvaa.

Kytkemällä volttimittari virrankiinnittimiin - kohdat 2 - 2 kuvassa.1, eli niihin resistanssin rx napoihin, joihin virtapiirin johdot on kytketty, saadaan volttimittarin lukema U «v pienempi kuin U'v liitäntäjohtojen jännitehäviön määrästä ja siksi löydetty halutun resistanssin arvo rx «= U»v / Ia = rx + 2 rk sisältää virheen, joka johtuu vain kosketusresistanssista.

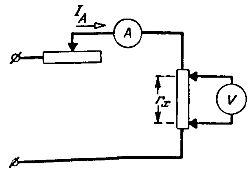
Kytkemällä volttimittarin kuvan 1 mukaisesti. 2, nykyisten välissä sijaitseviin potentiaaliliittimiin saadaan volttimittarin lukemat U»'v on pienempi kuin U «v kosketinresistanssien yli olevan jännitehäviön koosta ja siten vaaditun resistanssin löydetty arvo r»'x = U»v / Ia = rx

Riisi. 2. Oikea kytkentäkaavio pienten vastusten mittaamiseen ampeerimittarilla ja volttimittarilla

Siten löydetty arvo on yhtä suuri kuin vaaditun resistanssin todellinen arvo, koska volttimittari mittaa jännitteen todellisen arvon vaaditun resistanssin rx yli sen potentiaalisten napojen välillä.

Kahden puristimen, virran ja potentiaalin, käyttö on tärkein tekniikka, jolla eliminoidaan liitäntäjohtojen resistanssin ja transienttiresistanssien vaikutus pienten vastusten mittaustulokseen.

Suurten vastusten mittauksen ominaisuudet

Huonoilla virtajohtimilla ja eristimillä on korkea resistanssi. Kun mitataan johtojen vastusta alhaisella sähkönjohtavuudella, eristysmateriaaleissa ja niistä valmistetuissa tuotteissa on otettava huomioon tekijät, jotka voivat vaikuttaa niiden kestävyyteen.

Näitä tekijöitä ovat pääasiassa lämpötila, esimerkiksi sähköpahvin johtavuus 20 °C:n lämpötilassa on 1,64 x 10-13 1 / ohm ja lämpötilassa 40 °C 21,3 x 10-13 1 / ohm. Siten 20 °C lämpötilan muutos aiheutti 13-kertaisen muutoksen vastuksessa (johtavuudessa)!

Luvut osoittavat selvästi, kuinka vaarallista on aliarvioida lämpötilan vaikutusta mittaustuloksiin. Samoin erittäin tärkeä vastuksen suuruuteen vaikuttava tekijä on sekä testimateriaalin että ilman kosteus.

Myös virran tyyppi, jolla testi suoritetaan, testattavan jännitteen suuruus, jännitteen kesto jne., voivat vaikuttaa resistanssiarvoon.

Eristysmateriaalien ja niistä valmistettujen tuotteiden resistanssia mitattaessa on otettava huomioon myös virran mahdollisuus kulkea kahden reitin kautta:

1) testattavan materiaalin tilavuuden mukaan,

2) testattavan materiaalin pinnalle.

Materiaalin kyvylle johtaa sähkövirtaa tavalla tai toisella on ominaista resistanssin määrä, jonka virta kohtaa tässä vitsissä.

Vastaavasti on olemassa kaksi käsitettä: 1 cm3:lle materiaalin ominaisvastus ja 1 cm2:lle materiaalin pintaresistiivisyys.

Otetaan esimerkki havainnollistamiseksi.

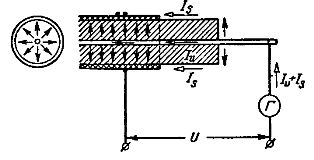
Mitattaessa kaapelin eristysresistanssia galvanometrillä, voi tapahtua suuria virheitä, koska galvanometri pystyy mittaamaan (kuva 3):

a) virta Iv, joka kulkee kaapelin ytimestä sen metallivaippaan eristeen tilavuuden läpi (kaapelin eristeen tilavuusresistanssista johtuva virta Iv luonnehtii kaapelin eristysresistanssia),

b) Virta, joka kulkee kaapelin sydämestä sen vaippaan eristyskerroksen pintaa pitkin (Koska pintaresistanssi ei riipu vain eristemateriaalin ominaisuuksista, vaan myös sen pinnan tilasta).

Riisi. 3. Kaapelin pinta- ja tilavuusvirta

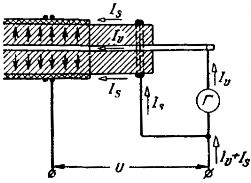
Johtavien pintojen vaikutuksen eliminoimiseksi eristysresistanssia mitattaessa kiinnitetään eristekerrokseen lankakela (turvarengas), joka liitetään kuvan 1 mukaisesti. 4.

Riisi. 4. Kaavio kaapelin tilavuusvirran mittaamiseksi

Tällöin virta Is kulkee galvanometrin lisäksi eikä tuo mittaustuloksiin virheitä.

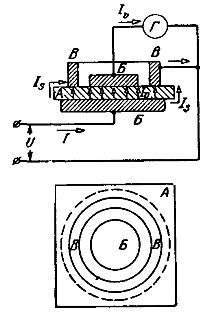
Kuvassa Kuvio 5 on kaaviokuva eristävän materiaalin bulkkiresistiivisuuden määrittämiseksi. — levyt A. Tässä BB — elektrodit, joihin syötetään jännite U, G — galvanometri, joka mittaa levyn A tilavuusresistanssista johtuvaa virtaa, V — suojarengas.

Riisi. 5. Kiinteän dielektrin tilavuusvastuksen mittaus

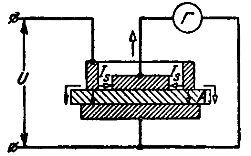
Kuvassa Kuva 6 on kaaviokuva eristävän materiaalin pintaresistanssin määrittämiseksi (levy A).

Riisi. 6. Kiinteän eristeen pintaresistanssin mittaus

Suuria resistanssia mitattaessa on kiinnitettävä vakavaa huomiota myös itse mittauslaitteiston eristykseen, koska muuten galvanometrin läpi kulkee itse asennuksen eristysvastuksen vuoksi virtaa, joka johtaa vastaavaan virheeseen mittauksessa.

Ennen mittaamista on suositeltavaa käyttää suojausta tai suorittaa mittausjärjestelmän eristystarkastus.