Potentiaalipiirikaavio

Potentiaalikaaviota kutsutaan graafiseksi esitykseksi sähköpotentiaalin jakautumisesta suljetussa silmukassa riippuen valitun silmukan sisältämien osien resistanssista.

Suljettu silmukka valitaan potentiaalikaavion muodostamiseksi. Tämä piiri on jaettu osiin siten, että jaksoa kohden on yksi käyttäjä tai energialähde. Osuuksien väliset rajakohdat on merkittävä kirjaimilla tai numeroilla.

Silmukan yksi piste on mielivaltaisesti maadoitettu, sen potentiaalin katsotaan ehdollisesti olevan nolla. Kun ääriviivaa kiertää myötäpäivään nollapotentiaalipisteestä, jokaisen seuraavan rajapisteen potentiaali määritellään edellisen pisteen potentiaalin ja näiden vierekkäisten pisteiden välisen potentiaalin muutoksen algebralliseksi summaksi.

Objektin potentiaalin muutos riippuu pisteiden välisen piirin koostumuksesta. Jos virrankuluttaja (vastus) sisältyy paikkaan, potentiaalin muutos on numeerisesti yhtä suuri kuin jännitehäviö tämän vastuksen yli. Tämän muutoksen etumerkki määräytyy virran suunnan mukaan.Jos silmukan virta- ja ohitussuunnat täsmäävät, etumerkki on negatiivinen, muuten se on positiivinen.

Jos objektissa on EMF-lähde, potentiaalinen muutos tässä on numeerisesti yhtä suuri kuin tämän lähteen EMF-arvo. Jos silmukan ohituksen suunta ja EMF:n suunta ovat samat, potentiaalimuutos on positiivinen, muuten negatiivinen.

Kun kaikkien pisteiden potentiaalit on laskettu, muodostetaan potentiaalikaavio suorakaiteen muotoiseen koordinaattijärjestelmään. Abskissa-akselilla osien resistanssit piirretään mittakaavassa siinä järjestyksessä, jossa ne kohtaavat ääriviivaa ylittäessään, ja ordinaatalla vastaavien pisteiden potentiaalit. Potentiaalikaavio alkaa nollapotentiaalista ja päättyy sen läpi kiertämisen jälkeen.

Muodosta potentiaalipiirikaavio

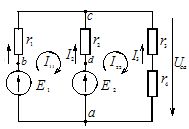
Tässä esimerkissä rakennamme potentiaalikaavion piirin ensimmäiselle silmukalle, jonka kaavio on esitetty kuvassa 1.

Riisi. 1. Monimutkaisen sähköpiirin kaavio

Tarkasteltava piiri sisältää kaksi teholähdettä E1 ja E2 sekä kaksi tehonkuluttajaa r1, r2.

Jaamme tämän ääriviivan osiin, joiden rajat on merkitty kirjaimilla a, b, c, d. Hiotamme pisteen a, tavanomaisesti pitäen sen potentiaalia nollana, ja ympyröimme ääriviivan myötäpäivään tästä pisteestä. Siksi φα = 0.

Seuraava piste polulla, joka ylittää ääriviivan, on piste b. EMF-lähde E1 sijaitsee osassa ab. Kun tässä osiossa siirrytään lähteen negatiivisesta positiiviseen napaan, potentiaali kasvaa arvolla E1:

φb = φa + E1 = 0 + 24 = 24 V

Kun siirrytään pisteestä b pisteeseen c, potentiaali pienenee vastuksen r1 yli olevan jännitehäviön koon verran (silmukan ohitussuunta on sama kuin vastuksen r1 virran suunta):

φc = φb — Az1r1 = 24 — 3 x 4 = 12V

Kun siirryt pisteeseen d, potentiaali kasvaa jännitehäviön verran vastuksen r2 yli (tässä osassa virran suunta on päinvastainen kuin silmukan ohituksen suunta):

φd = φ° C + I2r2 = 12 + 0 NS 4 = 12 V

Pisteen a potentiaali on pienempi kuin pisteen d potentiaali lähteen E2 EMF:n arvolla (EMF:n suunta on päinvastainen kuin piirin ohitussuunta):

φa = φd — E2 = 12 — 12 = 0

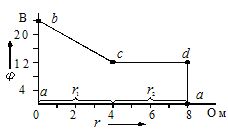
Laskelmien tuloksia käytetään potentiaalikaavion rakentamiseen. Abskissa-akselilla osien resistanssi piirretään sarjaan, kuten se olisi silloin, kun piiriä ympäröi nollapotentiaalipiste. Vastaavien pisteiden aiemmin lasketut potentiaalit piirretään ordinaatille (kuva 2).

Piirustus 2… Potentiaalikäyräkaavio

Patskevich V.A.