Jatkuvat värähtelyt ja parametrinen resonanssi

Jatkuvat värähtelyt – värähtelyt, joiden energia ei muutu ajan kuluessa. Todellisissa fysikaalisissa järjestelmissä on aina syitä, jotka aiheuttavat värähtelyenergian siirtymisen lämpöenergiaksi (esim. kitka mekaanisissa järjestelmissä, aktiivinen vastus sähköjärjestelmissä).

Siksi vaimentamattomia värähtelyjä voidaan saavuttaa vain, jos nämä energiahäviöt korvataan. Tällainen täydennys tapahtuu automaattisesti itsevärähtelevissä järjestelmissä ulkoisesta lähteestä tulevan energian vuoksi. Jatkuvat sähkömagneettiset värähtelyt ovat erittäin laajalti käytössä. Niiden saamiseksi käytetään erilaisia ​​generaattoreita.

Jotta sähköiset tai mekaaniset (värähtelevän ympyrän tai heilurin) värähtelyt vaimenettaisiin, vastus- tai kitkahäviöt on aina kompensoitava.

Voit esimerkiksi toimia värähtelevässä piirissä vaihtelevalla EMF:llä, joka lisää ajoittain kelan virtaa ja ylläpitää vastaavasti kondensaattorin jännitteen amplitudia.Tai voit työntää heiluria samalla tavalla pitäen sen heilumassa harmonisesti.

Kuten tiedät, värähtelypiirin käämin magneettikentän energian suuruus liittyy sen induktanssiin ja virtaan seuraavalla suhteella (toinen kaava onkondensaattorin sähkökentän energia sama ääriviiva)

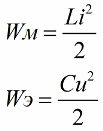
Ensimmäisestä kaavasta on selvää, että jos lisäämme ajoittain kelan virtaa, joka vaikuttaa vaihtuvaan EMF-piiriin, niin (lisäämällä tai vähentämällä kaavan toista tekijää - virtaa) täydennämme tätä piiriä ajoittain energialla.

Vaikuttamalla piiriin tiukasti ajassa sen luonnollisilla vapailla värähtelyillä, eli resonanssitaajuudella, saamme sähköisen resonanssin ilmiön, koska se on resonanssitaajuudella värähtelevä järjestelmä imee voimakkaimmin sille toimitetun energian.

Mutta entä jos muutat säännöllisesti ei toista tekijää (ei virtaa tai jännitettä), vaan ensimmäistä tekijää - induktanssia tai kapasitanssia? Tässä tapauksessa myös piirin energia muuttuu.

Esimerkiksi työntämällä sydäntä ajoittain sisään ja ulos kelasta tai työntämällä sisään ja ulos kondensaattoristadielektrinen, — saamme myös hyvin selvän jaksollisen muutoksen piirin energiassa.

Kirjoitamme tämän aseman kelan induktanssin yksikkömuutokselle:

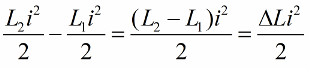
Selkein vaikutus piirin heilahtelulla on, jos induktanssin muutokset tehdään juuri ajoissa. Esimerkiksi, jos otamme saman piirin minä tahansa hetkenä, kun jonkin verran virtaa i jo kulkee sen läpi, ja viemme käämiin sydämen, niin energia muuttuu seuraavan määrän:

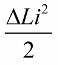
Anna nyt itse piirissä ilmaantua vapaita värähtelyjä, mutta sillä hetkellä, kun neljännesjakson jälkeen energia on mennyt kokonaan kondensaattoriin ja kelan virta on nolla, poistamme äkillisesti sydämen kelasta. Induktanssi palaa alkuperäiseen tilaansa, alkuarvoon L. Magneettikenttää vastaan ​​ei tarvitse tehdä työtä, kun ydin poistetaan. Siksi, kun ydin työnnettiin kelaan, piiri sai energiaa, koska työskentelimme, jonka arvo:

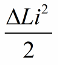
Neljänneksen jakson jälkeen kondensaattori alkaa purkautua, sen energia muuttuu jälleen käämin magneettikentän energiaksi.Kun magneettikenttä saavuttaa amplitudin, painamme ydintä taas jyrkästi. Jälleen induktanssi kasvoi, kasvoi samalla määrällä.

Ja jälleen, nollavirralla, palautamme induktanssin alkuperäiseen arvoonsa. Tämän seurauksena, jos kunkin puolijakson energianlisäykset ylittävät vastushäviöt, silmukan energia kasvaa koko ajan ja värähtelyamplitudi kasvaa. Tätä tilannetta ilmaisee eriarvoisuus:

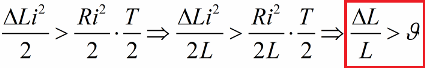
Tässä jaoimme tämän epäyhtälön molemmat puolet L:llä ja kirjoitimme ehdon parametrisen herätteen mahdollisuudelle hyppyillä tietylle logaritmisen dekrementin arvolle.

On suositeltavaa vaihtaa induktanssi (tai kapasitanssi) kahdesti jaksossa, joten parametrin muutoksen taajuuden (parametrisen resonanssitaajuuden) tulee olla kaksi kertaa värähtelevän järjestelmän luonnollinen taajuus:

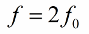
Joten värähtelyjen virityspolku piirissä on ilmaantunut ilman, että EMF:ää tai virtaa on tarpeen muuttaa suoraan.Alkuvaihtelu virtapiirissä on aina tavalla tai toisella läsnä, eikä siinä edes oteta huomioon ilmakehän radiotaajuisten värähtelyjen aiheuttamia häiriöitä.

Jos induktanssi (tai kapasitanssi) ei muutu hyppyissä, vaan harmonisesti, värähtelyjen esiintymisen ehto näyttää hieman erilaiselta:

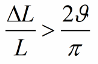
Koska kapasitanssi ja induktanssi ovat piiriparametreja (kuten heilurin massa tai jousen kimmoisuus), värähtelyn herätysmenetelmää kutsutaan myös parametriseksi viritykseksi.

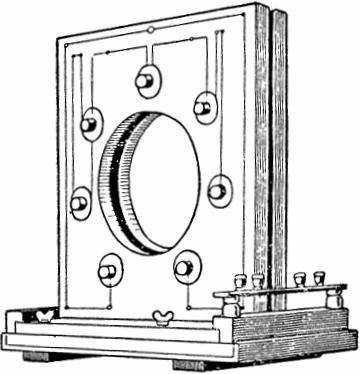
Tämän ilmiön löysivät ja käytännössä tutkivat 1900-luvun alussa Neuvostoliiton fyysikot Mandelstam ja Papalexi. Tämän fyysisen ilmiön perusteella he rakensivat ensimmäisen parametrisen AC-generaattorin, jonka teho oli 4 kW ja muuttuva induktio.

Generaattorin suunnittelussa rungon molemmilla puolilla oli seitsemän paria litteitä keloja, joiden ontelossa pyöri ferromagneettinen kiekko ulkonemilla. Kun levyä pyöritetään moottorilla, sen ulkonemat liikkuvat ajoittain kunkin kelaparin välisessä tilassa ja muuttaen siten induktanssia ja jännittäviä värähtelyjä.