Elektroni sähkökentässä

Elektronin liike sähkökentässä on yksi tärkeimmistä sähkötekniikan fysikaalisista prosesseista. kuva Katsotaanpa, kuinka tämä tapahtuu tyhjiössä. Tarkastellaan ensin esimerkkiä elektronin liikkeestä katodilta anodille tasaisessa sähkökentässä.

Alla oleva kuva näyttää tilanteen, jossa elektroni poistuu negatiivisesta elektrodista (katodista) merkityksettömän pienellä alkunopeudella (nollaan) ja menee sisään yhtenäisessä sähkökentässäkahden elektrodin välissä.

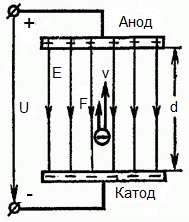
Elektrodeihin kohdistuu vakiojännite U ja sähkökentällä on vastaava voimakkuus E. Elektrodien välinen etäisyys on yhtä suuri kuin d. Tässä tapauksessa elektroniin vaikuttaa kentän puolelta voima F, joka on verrannollinen elektronin varaukseen ja kentän voimakkuuteen:

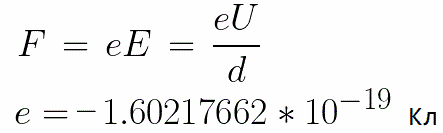
Koska elektronilla on negatiivinen varaus, tämä voima kohdistuu kentänvoimakkuusvektoria E vastaan. Vastaavasti elektroni kiihtyy tähän suuntaan sähkökentän vaikutuksesta.

Elektronin kokema kiihtyvyys on verrannollinen siihen vaikuttavan voiman F suuruuteen ja kääntäen verrannollinen elektronin massaan m.Koska kenttä on tasainen, tietyn kuvan kiihtyvyys voidaan ilmaista seuraavasti:

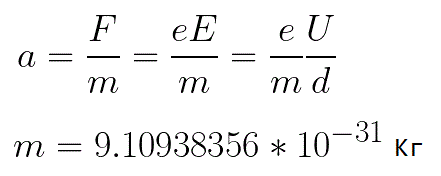
Tässä kaavassa elektronin varauksen suhde sen massaan on elektronin ominaisvaraus, määrä, joka on fysikaalinen vakio:

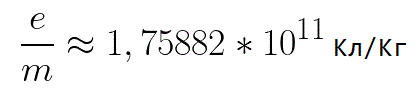
Elektroni on siis kiihtyvässä sähkökentässä, koska alkunopeuden v0 suunta osuu yhteen kentän puolella olevan voiman F suunnan kanssa ja siksi elektroni liikkuu tasaisesti. Jos esteitä ei ole, se kulkee elektrodien välistä polkua d ja saavuttaa anodin (positiivisen elektrodin) tietyllä nopeudella v. Sillä hetkellä, kun elektroni saavuttaa anodin, sen kineettinen energia on vastaavasti yhtä suuri kuin:

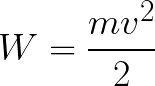
Koska elektroni kiihtyy koko polulla d sähkökentän voimien vaikutuksesta, se saa tämän kineettisen energian kentän sivuun vaikuttavan voiman tekemän työn tuloksena. Tämä työ vastaa:

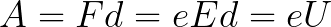
Tällöin kentässä liikkuvan elektronin hankkima kineettinen energia voidaan löytää seuraavasti:

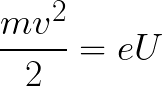
Eli ei ole mitään muuta kuin kenttävoimien työ kiihdyttää elektronia pisteiden välillä, joiden potentiaaliero on U.

Tällaisissa tilanteissa elektronin energian ilmaisemiseksi on kätevää käyttää sellaista mittayksikköä kuin "elektronivoltti", joka on yhtä suuri kuin elektronin energia 1 voltin jännitteellä. Ja koska elektronin varaus on vakio, niin 1 elektrovoltti on myös vakioarvo:

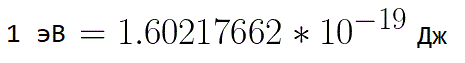
Edellisestä kaavasta voit helposti määrittää elektronin nopeuden missä tahansa pisteessä sen tiellä liikkuessaan kiihtyvässä sähkökentässä, kun tiedät vain sen potentiaalieron, jonka se ohitti kiihtyessään:

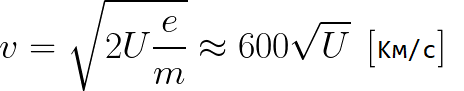
Kuten näemme, elektronin nopeus kiihtyvässä kentässä riippuu vain polun loppupisteen ja alkupisteen välisestä potentiaalierosta U.

Kuvittele, että elektroni alkaa liikkua pois katodista mitättömällä nopeudella ja katodin ja anodin välinen jännite on 400 volttia. Tässä tapauksessa anodin saavuttamishetkellä sen nopeus on yhtä suuri:

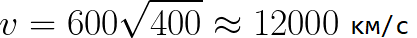
On myös helppo määrittää aika, joka elektronin tarvitsee kulkea elektrodien välisen matkan d. Tasaisesti kiihdytetyllä liikkeellä levosta keskinopeudeksi havaitaan puolet loppunopeudesta, jolloin kiihdytetyn lennon aika sähkökentässä on yhtä suuri:

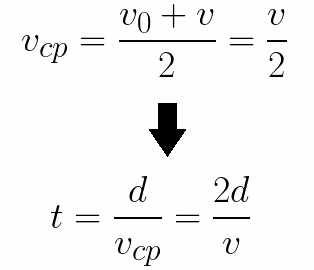
Tarkastellaan nyt esimerkkiä, jossa elektroni liikkuu hidastuvassa tasaisessa sähkökentässä eli kenttä on suunnattu kuten ennenkin, mutta elektroni alkaa liikkua vastakkaiseen suuntaan - anodilta katodille.

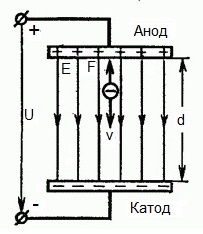
Oletetaan, että elektroni poistui anodista jollain alkunopeudella v ja lähti aluksi liikkumaan katodin suuntaan. Tässä tapauksessa sähkökentän puolelta elektroniin vaikuttava voima F suunnataan sähköistä intensiteettivektoria E vastaan ​​- katodilta anodille.

Se alkaa hidastaa elektronin alkunopeutta, eli kenttä hidastaa elektronia. Tämä tarkoittaa, että elektroni näissä olosuhteissa alkaa liikkua tasaisesti ja tasaisesti hitaasti. Tilannetta kuvataan seuraavasti: "elektroni liikkuu hidastuvassa sähkökentässä."

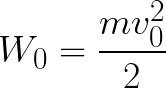
Anodilta elektroni alkoi liikkua nollasta poikkeavalla kineettisellä energialla, joka alkaa pienentyä hidastuessa, koska energiaa kuluu nyt kentästä elektroniin vaikuttavan voiman voittamiseen.

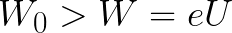
Jos elektronin alkuperäinen kineettinen energia sen poistuessaan anodista oli välittömästi suurempi kuin energia, joka kentän on kulutettava nopeuttaakseen elektronin siirtymistä katodilta anodille (kuten ensimmäisessä esimerkissä), elektroni kulkea matkan d ja saavuttaa lopulta katodin jarrutuksesta huolimatta.

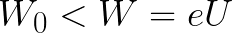
Jos elektronin kineettinen alkuenergia on pienempi kuin tämä kriittinen arvo, elektroni ei saavuta katodia. Tietyssä kohdassa se pysähtyy ja alkaa sitten tasaisesti kiihdytetty liike takaisin anodille. Seurauksena on, että kenttä palauttaa sille pysäytysprosessiin käytetyn energian.

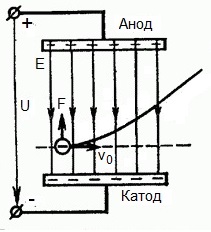
Mutta entä jos elektroni lentää nopeudella v0 suorassa kulmassa sähkökentän vaikutusalueella? Ilmeisesti tällä alueella kentän puolella oleva voima on suunnattu elektronille katodista anodille, eli sähkökentän voimakkuusvektoria E vastaan.

Tämä tarkoittaa, että nyt elektronilla on kaksi liikekomponenttia: ensimmäinen - nopeudella v0 kohtisuorassa kenttää vastaan, toinen - tasaisesti kiihtyvä voiman vaikutuksesta kentän puolelta, joka on suunnattu anodia kohti.

Osoittautuu, että lentäessään toimintakentälle elektroni liikkuu parabolista lentorataa pitkin. Mutta kun elektroni on lentänyt pois kentän toiminta-alueelta, se jatkaa tasaista liikettään inertialla suoraviivaista liikerataa pitkin.