Sähkömagneettien vetovoima

Voima, jolla sähkömagneetti vetää puoleensa ferromagneettisia materiaaleja, riippuu magneettivuosta F tai vastaavasti induktiosta B ja sähkömagneetin S poikkileikkauspinta-alasta.

Sähkömagneetin painevoima määräytyy kaavan mukaan

F = 40550 ∙ B ^ 2 ∙ S,

jossa F on sähkömagneetin painevoima, kg (voima mitataan myös newtoneina, 1 kg = 9,81 N tai 1 N = 0,102 kg); B - induktio, T; S on sähkömagneetin poikkipinta-ala, m2.

Esimerkkejä

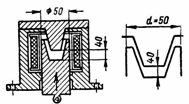
1. Hanan sähkömagneetti on magneettinen piiri (kuva 1). Mikä on hevosenkenkänosturin sähkömagneetin nostovoima, jos magneettinen induktio on B = 1 T ja sähkömagneetin jokaisen navan poikkipinta-ala on S = 0,02 m2 (kuva 1, b)? Jätä huomioimatta sähkömagneetin ja ankkurin välisen raon vaikutus.

Riisi. 1. Nostoelektromagneetti

F = 40550 ∙ B ^ 2 ∙ S; F = 40550 ∙ 1 ^ 2 ∙ 2 ∙ 0,02 = 1622 kg.

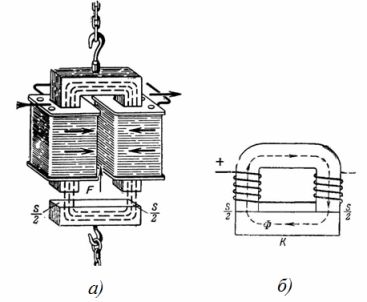
2. Pyöreän terässähkömagneetin mitat ovat kuvan 1 mukaiset. 2, a ja b. Sähkömagneetin nostovoima on 3 T. Määritä sähkömagneetin sydämen poikkipinta-ala, n. p. ja käämin kierrosten lukumäärä magnetointivirralla I = 0,5 A.

Riisi. 2. Pyöreä sähkömagneetti

Magneettivuo kulkee pyöreän sisäytimen läpi ja palaa sylinterimäisen rungon läpi. Sydämen Sc ja kotelon Sk poikkileikkausalat ovat suunnilleen samat, joten induktioarvot sydämessä ja kotelossa ovat käytännössä samat:

Sc = (π ∙ 40 ^ 2) / 4 = (3,14 ∙ 1600) / 4 = 1256 cm2 = 0,1256 m2,

Sk = ((72 ^ 2-60 ^ 2) ∙ π) / 4 = 3,14 / 4 ∙ (5184-3600) = 1243,5 cm2 = 0,12435 m2;

S = Sc + Sk = 0,24995 m2 ≈0,25 m2.

Tarvittava induktio sähkömagneetissa määritetään kaavalla F = 40550 ∙ B ^ 2 ∙ S,

jossa B = √ (F / (40550 ∙ S)) = √ (3000 / (40550 ∙ 0,25)) = 0,5475 T.

Tämän induktion jännite löytyy valuteräksen magnetointikäyrästä:

H = 180 A/m.

Kenttäviivan keskimääräinen pituus (kuva 2, b) lav = 2 ∙ (20 + 23) = 86 cm = 0,86 m.

Magnetointivoima I ∙ ω = H ∙ lav = 180 ∙ 0,86 = 154,8 Av; I = (I ∙ ω) / I = 154,8 / 0,5 = 310 A.

Itse asiassa n. s eli virran ja kierrosten lukumäärän on oltava monta kertaa suurempi, koska sähkömagneetin ja ankkurin välillä on väistämätön ilmarako, mikä lisää merkittävästi magneettipiirin magneettista vastusta. Siksi ilmarako on otettava huomioon sähkömagneetteja laskettaessa.

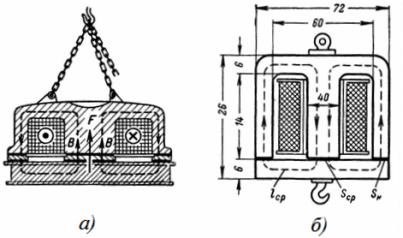
3. Hanan sähkömagneetin kelassa on 1350 kierrosta, jonka läpi kulkee virta I = 12 A. Sähkömagneetin mitat on esitetty kuvassa. 3. Minkä painon sähkömagneetti nostaa 1 cm:n etäisyydellä armatuurista ja minkä painon se kestää painovoiman jälkeen?

Riisi. 3. Sähkömagneettinen kela

Suurin osa N.:sta, jonka I ∙ ω kuluu magneettivuon johtamiseen ilmaraon läpi: I ∙ ω≈Hδ ∙ 2 ∙ δ.

Magnetointivoima I ∙ ω = 12 ∙ 1350 = 16200 A.

Koska H ∙ δ = 8 ∙ 10 ^ 5 ∙ B, niin Hδ ∙ 2 ∙ δ = 8 ∙ 10 ^ 5 ∙ B ∙ 0,02.

Siksi 16200 = 8 ∙ 10 ^ 5 ∙ B ∙ 0,02, ts. B = 1,012T.

Oletetaan, että induktio on B = 1 T, koska osa n:stä. c. I ∙ ω käytetään magneettivuon johtamiseen teräksessä.

Tarkistetaan tämä laskelma kaavalla I ∙ ω = Hδ ∙ 2 ∙ δ + Hс ∙ lс.

Magneettiviivan keskimääräinen pituus on: lav = 2 ∙ (7 + 15) = 44 cm = 0,44 m.

Intensiteetti Hc kohdassa B = 1 T (10000 Gs) määritetään magnetointikäyrästä:

Hc = 260 A / m. I ∙ ω = 0,8 ∙ B ∙ 2 + 2,6 ∙ 44 = 1,6 ∙ 10 000 + 114,4 = 16114 Av.

Magnetointivoima I ∙ ω = 16114 Av muodostaen induktion B = 1 T on käytännössä yhtä suuri kuin annettu n. v. I ∙ ω = 16200 Av.

Sydämen ja kartion kokonaispoikkipinta-ala on: S = 6 ∙ 5 + 2 ∙ 5 ∙ 3 = 0,006 m2.

Sähkömagneetti vetää puoleensa varauksen, jonka paino on F = 40550 ∙ B ^ 2 ∙ S = 40550 ∙ 1 ^ 2 ∙ 0,006 = 243,3 kg 1 cm:n etäisyydeltä.

Koska ilmarako käytännössä katoaa ankkurin vetäytymisen jälkeen, sähkömagneetti kestää paljon suuremman kuormituksen. Tässä tapauksessa koko n. c. I ∙ ω kuluu magneettivuon johtamiseen vain teräksessä, joten I ∙ ω = Hс ∙ lс; 16200 = Hs ∙ 44; Hc = 16200/44 = 368 A/cm = 36800 A/m.

Tällaisella jännitteellä teräs on käytännössä kyllästynyt ja induktio siinä on noin 2 T. Sähkömagneetti vetää puoleensa ankkuria voimalla F = 40550 ∙ B ^ 2 ∙ S = 40550 ∙ 4 ∙ 0,006 = 973 kg.

4. Signaalirele (vilkkurele) koostuu panssaroidusta sähkömagneetista 1, jossa on pyöreä ydin ja venttiilityyppinen ankkuri 2, joka syötettyään sähkömagneetille virran vetää puoleensa ja vapauttaa vilkkulaitteen 3, joka avaa signaalinumeron (kuva 1). 4).

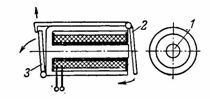
Riisi. 4. Panssari sähkömagneetti

Magnetointivoimakkuus on I ∙ ω = 120 Av, ilmarako δ = 0,1 cm ja sähkömagneetin kokonaispoikkipinta-ala on S = 2 cm2. Arvioi releen vetovoima.

Induktanssi B määritetään peräkkäisillä approksimaatioilla käyttämällä yhtälöä I ∙ ω = Hс ∙ lс + Hδ ∙ 2 ∙ δ.

Olkoon n. c. Hc∙lc on 15 % I∙ ω, ts. 18 Av.

Silloin I ∙ ω-Hс ∙ lс = Hδ ∙ 2 ∙ δ; 120-18 = H8 ∙ 0,2; Hδ = 102/0,2 = 510 A/cm = 51000 A/m.

Tästä syystä löydämme induktion B:

Hδ = 8 ∙ 10 ^ 5 V; B = Hδ / (8 ∙ 10 ^ 5) = 51 000 / (8 ∙ 10 ^ 5) = 0,0637 T.

Kun arvo B on korvattu kaavassa F = 40550 ∙ B ^ 2 ∙ S, saadaan:

F = 40550 ∙ 0,0637 ^ 2 ∙ 0,0002 = 0,0326 kg.

5. DC-jarrun solenoidissa (kuva 5) on männän ankkuri kartiomaisella rajoittimella. Ankkurin ja sydämen välinen etäisyys on 4 cm. Työhalkaisija (ympyränmuotoiset ytimet) d = 50 mm. Ankkuria vedetään kelaan 50 kg voimalla. Keskivoimalinjan pituus lav = 40 cm. Määritä n. s. ja kelan virta, jos kierrosta on 3000.

Riisi. 5. DC-jarrun solenoidi

Sähkömagneetin työosan pinta-ala on yhtä suuri kuin ympyrän pinta-ala, jonka halkaisija on d = 5 cm:

S = (π ∙ d ^ 2) / 4 = 3,14 / 4 ∙ 25 = 19,6 cm2.

Voiman F = 50 kg synnyttämiseen tarvittava induktio B saadaan yhtälöstä F = 40550 ∙ B ^ 2 ∙ S,

jossa B = √ (F / (40550 ∙ S)) = √ (50 / (40550 ∙ 0,00196)) = 0,795 T.

Magnetointivoima I ∙ ω = Hс ∙ lс + Hδ ∙ δ.

Määritämme teräksen Hc ∙ lc magnetointilujuuden yksinkertaistetusti perustuen siihen, että se on 15 % I ∙ ω:

I ∙ ω = 0,15 ∙ I ∙ ω + Hδ ∙ δ; 0,85 ∙ I ∙ ω = Hδ ∙ δ; 0,85 ∙ I ∙ ω = 8 ∙ 10 ^ 5 ∙ B ∙ δ; I ∙ ω = (8 ∙ 10 ^ 5 ∙ 0,795 ∙ 0,04) / 0,85 = 30 000 Av.

Magnetointivirta I = (I ∙ ω) / ω = 30000/3000 = 10 A.