Kondensaattorin kapasitanssin laskeminen

Kapasitanssi C on kondensaattorin kyky vastaanottaa (varastoida ja säilyttää) sähkömäärä Q ampeerisekunteina tai varaus Q riipuksissa. Jos kerrot kappaleelle, esimerkiksi pallolle, sähkövarauksen (sähkön määrä) Q, niin tämän kappaleen ja maan väliin kytketty sähköskooppi näyttää jännitteen U (kuva 1). Tämä jännite on verrannollinen varaukseen ja riippuu myös rungon muodosta ja koosta.

Varauksen Q ja jännitteen U välinen suhde ilmaistaan ​​kaavalla Q = C ∙ U.

Suhteellisuusvakiota C kutsutaan kappaleen kapasitanssiksi. Jos runko on pallon muotoinen, kappaleen kapasitanssi on verrannollinen pallon säteeseen r.

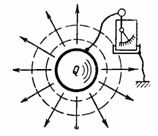
Riisi. 1.

Kapasitanssin mittayksikkö on farad (F).

Kapasitanssi on 1 F, kun 1 k:n varaus tuottaa 1 V:n jännitteen sen ja maan välille. Faradit ovat erittäin suuri mittayksikkö, joten käytännössä käytetään pienempiä yksiköitä: microfarad (μF), nanofarad (nF) ja picofarad (pF)...

Nämä yksiköt liittyvät toisiinsa seuraavilla suhteilla: 1 Ф = 10 ^ 6 μF; 1 µF = 10^ 6 pF; 1 nF = 10^3 pF.

1 cm:n säteellä olevan pallon kapasitanssi on 1,1 pF.

Ei vain eristetty kappale voi kerätä varausta, vaan myös erityinen laite, jota kutsutaan kondensaattoriksi. Kondensaattori koostuu kahdesta tai useammasta levystä (levystä), jotka on erotettu eristeellä (eriste).

Kuvassa Kuva 2 esittää piirin, jossa DC-lähde on kytketty kondensaattoriin. Kytkettäessä kondensaattorin oikeaan levyyn muodostuu positiivinen varaus +Q ja vasempaan levyyn negatiivinen varaus -Q. Aikana kondensaattorin lataus piirin läpi kulkee virta, joka pysähtyy latauksen päätyttyä; silloin kondensaattorin yli oleva jännite on yhtä suuri kuin e. jne. c. lähde U. Kondensaattorilevyn varaus, jännite ja kapasitanssi ovat suhteessa Q = C ∙ U. Tällöin kondensaattorin eristeeseen muodostuu sähköstaattinen kenttä.

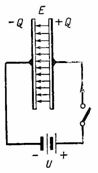
Riisi. 2.

Ilmaeristeellä varustetun kondensaattorin kapasiteetti voidaan laskea kaavalla C = S / (4 ∙ π ∙ d) ∙ 1,11, pF, missä S on yhden levyn pinta-ala, cm2; d on levyjen välinen etäisyys, cm; C on kondensaattorin kapasitanssi, pF.

N:stä levystä koostuvan kondensaattorin kapasiteetti (kuva 3) on yhtä suuri kuin: C = (n-1) ∙ S / (4 ∙ π ∙ d) ∙ 1,11, pF.

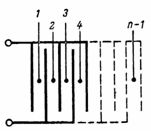
Riisi. 3.

Jos levyjen välinen tila täytetään toisella eristeellä, esimerkiksi paperilla, kondensaattorin kapasitanssi kasvaa kertoimella ε. Kun käytetään paperieristystä, kapasiteetti kasvaa 3 kertaa, kiilleeristeellä - 5-8 kertaa, lasilla - 7 kertaa jne. ε:n arvoa kutsutaan eristeen dielektrisyysvakioksi.

Yleinen kaava kondensaattorin kapasitanssin määrittämiseksi dielektrisyysvakiolla ε (epsilon) on: C = ε ∙ S / (4 ∙ π ∙ d) ∙ 1,11, pF.

Tämä kaava on hyödyllinen radioiden pienten muuttuvien kondensaattorien laskemiseen.Sama kaava voidaan esittää seuraavasti: C = (ε_0 ∙ ε ∙ S) / d, missä ε_0 on tyhjön dielektrisyysvakio tai dielektrisyysvakio (ε_0 = 8,859 ∙ 10 ^ (- 12) F / m); ε on eristeen dielektrisyysvakio.

Tässä kaavassa mitat korvataan metreinä ja kapasitanssi saadaan faradeina.

Esimerkkejä

1. Mikä on maaplaneetan kapasiteetti, jonka säde on r = 6378 km?

Koska pallon, jonka säde on 1 cm, kapasitanssi on 1,11 pF, maan kapasitanssi on: C = 637,8 ∙ 10 ^ 6 ∙ 1,11 = 707,95 ∙ 10 ^ 6 pF = 708 μ. (Planeettamme kokoisen pallon kapasiteetti on suhteellisen pieni. Pienkokoisilla elektrolyyttikondensaattoreilla on tämä kapasiteetti).

2. Määritä kahdesta levystä koostuvan kondensaattorin kapasitanssi, joiden kummankin pinta-ala on S = 120 cm2.

Levyt erottaa ilmakerros, jonka paksuus on d = 0,5 cm, C = S / (4 ∙ π ∙ d) ∙ 1,11 = (120 ∙ 1,11) / (4 ∙ π ∙ 0,5) = 21 ,20 pF ...

3. Määritä kondensaattorin kapasitanssi edellisessä esimerkissä annetuilla tiedoilla, jos levyjen välinen tila on täytetty vahapaperilla, jonka dielektrisyysvakio ε = 4, lasilla (ε = 7), sähköpahvilla (ε = 2) , kiille (e = 8).

Vahapaperikondensaattorin kapasitanssi on C = ε ∙ (S ∙ 1,11) / (4 ∙ π ∙ d) = 4 ∙ 21,2 = 84,8 pF.

Lasikondensaattorin kapasitanssi on C = 7 ∙ 21,2 = 148,4 pF.

Pahvikondensaattorin kapasitanssi on C = 2 ∙ 21,2 = 42,3 pF.

Kiillekondensaattorin kapasitanssi on C = 8 ∙ 21,2 = 169,6 pF.

4. Mikä on kiertoilmakondensaattorin kapasitanssi radiovastaanottimelle, joka koostuu 20 levystä, joiden pinta-ala on 20 cm2, jos levyjen välinen etäisyys on 0,06 cm (kuva 149)?

C = (n-1) ∙ (S ∙ 1,11) / (4 ∙ π ∙ d) = (20-1) ∙ (20 ∙ 1,11) / (4 ∙ π ∙ 0,06) = 559, 44 pF.

Kuvassa näkyvä kondensaattori.3, koostuu erillisistä yksinkertaisimmista kondensaattoreista, joissa on kaksi levyä, joiden lukumäärä on n-1.

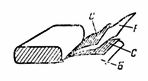
5. Paperikondensaattori, jonka kapasitanssi on C = 2 μF, koostuu kahdesta folioliuskasta C ja kahdesta eristeliuskasta vahapaperista B, jonka dielektrisyysvakio ε = 6. Vahapaperin paksuus on d = 0,1 mm. Taitetut nauhat rullataan, johdot valmistetaan teräslevyistä. Määritä lauhduttimen teräsnauhan pituus, jos sen leveys on 4 cm (kuva 4).

Riisi. 4.

Ensin määritetään yhden nauhan pinta-ala kaavalla C = ε ∙ S / (4 ∙ π ∙ d) ∙ 1,11, josta S = (C ∙ 4 ∙ π ∙ d) / (ε ∙ 1,11) = ( 2 ∙ 4 ∙ π ∙ 0,01 ∙ 10 ^ 6) / (6 ∙ 1,11); S = 2 000 000 / (6 ∙ 1,11) ∙ 4 ∙ π ∙ 0,01 = 37 680 cm2.

Kunkin nauhan pituus on l = 37680/4 = 9420 cm = 94,2 m.