Virtojen resonanssi

Kondensaattorin ja induktorin rinnakkaiskytkentä vaihtovirtapiirissä

Mieti ketjun ilmiöitä vaihtovirtajoka sisältää rinnankytketyn generaattorin, kondensaattorin ja kelan. Oletetaan, että piirissä ei ole aktiivista vastusta.

Selvästikin tällaisessa piirissä sekä kelan että kondensaattorin jännite milloin tahansa on yhtä suuri kuin generaattorin kehittämä jännite.

Piirin kokonaisvirta koostuu sen haaroissa olevista virroista. Induktiivisen haaran virta jää vaihejännitteestä neljänneksellä jaksosta ja kapasitiivisen haaran virta johtaa sitä saman jakson neljänneksen verran. Siksi haarojen virrat millä tahansa ajanhetkellä osoittautuvat vaihesiirretyiksi suhteessa toisiinsa puolella jaksolla, eli ne ovat vastavaiheessa. Siten haarojen virrat milloin tahansa suunnataan toisiaan kohti, ja kokonaisvirta piirin haarautumattomassa osassa on yhtä suuri kuin niiden ero.

Tämä antaa meille oikeuden kirjoittaa yhtäläisyys I = IL -integraalipiiri

missä minä- piirin kokonaisvirran tehollinen arvo, I L ja integroitu piiri - haarojen virtojen teholliset arvot.

Käyttämällä Ohmin lakia määrittämään virran teholliset arvot haaroissa, saamme:

Il = U / XL ja Az° C = U / XC

Jos piiriä hallitsee induktiivinen vastus, esim. XL Lisää ▼ XC, kelan virta on pienempi kuin kondensaattorin virta; siksi virta piirin haarautumattomassa osassa on luonteeltaan kapasitiivinen ja generaattorin piiri kokonaisuudessaan on kapasitiivinen. Kääntäen, kun XC on suurempi kuin XL, kondensaattorin virta on pienempi kuin kelan virta; siksi virta piirin haarautumattomassa osassa on induktiivinen ja generaattorin piiri kokonaisuudessaan on induktiivinen.

Ei pidä unohtaa, että molemmissa tapauksissa kuorma on reaktiivinen, ts. piiri ei kuluta generaattorin tehoa.

Virtojen resonanssi

Tarkastellaan nyt tapausta, jolloin rinnankytketyt kondensaattorit ja kela osoittautuivat reaktanssiltaan yhtäläisiksi, ts. Xll = X°C.

Jos oletetaan, kuten aiemmin, että käämillä ja kondensaattorilla ei ole aktiivista vastusta, niin jos niiden reaktiot ovat yhtä suuret (YL = Y° C), kokonaisvirta piirin haarautumattomassa osassa on nolla, kun taas haaroissa yhtä suuri virtaukset kulkevat suurimmalla voimakkuudella. Tässä tapauksessa piirissä tapahtuu resonanssivirtojen ilmiö.

Virtaresonanssissa kunkin haaran virtojen teholliset arvot, jotka määritetään suhteilla IL = U / XL ja Аz° С = U / XC, ovat keskenään yhtä suuret, joten XL = XC.

Päätelmä, jonka päätimme, saattaa tuntua ensi silmäyksellä melko oudolta. Itse asiassa generaattori on kuormitettu kahdella vastuksella, eikä piirin haarautuneessa osassa ole virtaa, kun taas samat ja lisäksi suurimmat virrat kulkevat itse vastuksissa.

Tämä selittyy kelan magneettikentän käyttäytymisellä ja kondensaattorin sähkökenttä… Virtojen resonanssilla, kuten jänniteresonanssi, kelan kentän ja kondensaattorin kentän välillä on energian vaihtelu. Generaattori näyttää olevan eristetty sen jälkeen, kun se on siirtänyt energian piiriin. Se voidaan kytkeä kokonaan pois päältä ja virta piirin haaroittuneessa osassa säilyy ilman generaattoria sillä energialla, jonka piiri alun perin varastoi. Myös jännite piirin napojen yli pysyy täsmälleen samana kuin generaattorin kehittämä jännite.

Siten kun induktori ja kondensaattori kytketään rinnan, saatiin oskillaattoripiiri, joka eroaa edellä esitetystä vain siinä, että värähtelyjä aiheuttavaa generaattoria ei ole kytketty suoraan piiriin ja piiri on suljettu. 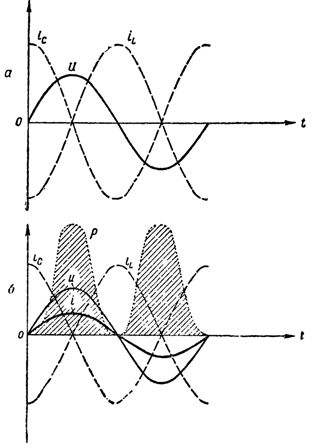Piirin virtojen, jännitteen ja tehon kuvaajat virtojen resonanssissa: a — aktiivinen vastus on nolla, piiri ei kuluta energiaa; b — piirissä on aktiivinen vastus, virta on ilmaantunut piirin haarautumattomaan osaan, piiri kuluttaa energiaa

L, C ja e, joissa virran resonanssi tapahtuu, määritetään, kuten jänniteresonanssissa (jos jätämme huomiotta piirin aktiivisen vastuksen), yhtälöllä:

ωL = 1 / ω° C

Siksi:

eres = 1/2π√LC

Lres = 1 / ω2C

Kappale = 1 / ω2L

Muuttamalla mitä tahansa näistä kolmesta suureesta voidaan saavuttaa yhtäläisyys Xl = X° C, eli muuttaa piiri värähteleväksi piiriksi.

Meillä on siis suljettu värähtelypiiri, jossa voimme indusoida sähköisiä värähtelyjä, ts. vaihtovirta. Ja jos ei olisi aktiivista vastusta, joka jokaisessa värähtelevässä piirissä on, vaihtovirta voisi olla jatkuvasti siinä.Aktiivisen vastuksen läsnäolo johtaa siihen, että piirin värähtelyt vaimentuvat vähitellen, ja niiden ylläpitämiseksi tarvitaan energialähde - vaihtovirtageneraattori.

Ei-sinimuotoisissa virtapiireissä resonanssimoodit ovat mahdollisia erilaisille harmonisille komponenteille.

Resonanssivirtoja käytetään laajasti käytännössä. Virtaresonanssi-ilmiötä käytetään kaistanpäästösuodattimissa sähköisenä "puristimena", joka viivästyttää tiettyä taajuutta. Koska taajuudella f on merkittävä virtavastus, jännitehäviö piirissä taajuudella f on suurin. Tätä silmukan ominaisuutta kutsutaan selektiivisyydeksi, sitä käytetään radiovastaanottimissa tietyn radioaseman signaalin eristämiseen. Virtojen resonanssitilassa toimiva värähtelypiiri on yksi pääkomponenteista elektroniset generaattorit.